Bài 1: Cho tứ giác ABCD gọi G là giao điểm của AC và BD. Gọi $O_1, O_2, O_3, O_4$ lần lượt là tâm của $ GAB, GBC. GCD, GDA$. Đường thẳng bất kì qua G cắt $(O_2), (O_4)$ tại J và K. Đường thẳng bất kì khác qua G cắt $(O_1), (O_3)$ tại $S$ và $T$. Gọi M là giao của $O_1O_2$ và $O_3O_4$, U, I là trung điểm ST và JK. Chứng minh rằng $MU=MI$.
Lời giải:
Gọi giao điểm thứ hai của $(O_1), (O_3)$ là Q, $(O_2), (O_4)$ là P. E, F là trung điểm AC, BD. Ta sẽ chứng minh G,E, F, P, Q cùng thuộc $w$
Xét phép vị tự quay tâm P biến B thành D, A thành C nên biến BD thành AC. Do E, F là trung điểm AC và BD nên biến E thành F, Suy ra tam giác APE đồng dạng PBF
Suy ra: $\widehat{PEG}=\widehat{PFG}$ nên tứ giác PGEF nội tiếp
Tương tự ta có tứ giác QGEF nội tiếp.
Ta có $O_2O_4$, $O_1O_3$ là trung trực của PG và GQ. nên M là tâm ngoại tiếp của 5 điểm P, Q, G, E, F.
Mặt khác tiếp tục xét phép vị tự quay tâm P biến S thành T và do I là trung điểm ST nên phép vị tự quay này biến I thành trung điểm F của BD nên tam giác IPS đồng dạng tam giác PFB. Suy ra $\widehat{PIG}=\widehat{PFG}$ Suy ra I thuộc đường tròn tâm M. Tương tự U cũng thuộc đường tròn tâm M.
Vậy MI=MU
Nhận xét: Nếu tứ giác ABCD nội tiếp (O) thì ta có OE và OF lần lượt vuông AC và BD, suy ra M là trung điểm PO. Suy ra OG vuông GP ( vì G thuộc đường tròn đường kính PO) Và đây là đề thi Trung Quốc 1992.
Bài 2 (Đề thi chọn đội tuyển Thụy Sĩ): Cho tam giác ABC nội tiếp (O), trực tâm H. D, E trên AB, AC sao cho D, H, E thẳng hàng và tam giác ADE cân tại A. (ADE) cắt (O) tại G. Chứng minh GH vuông GA.
Lời giải:
Gọi BB', CC' là các đường cao của tam giác ABC. R là giao của (AB'C') và (ABC) thì HMR thẳng hàng và HR vuông AR. Ta sẽ chứng minh R thuộc (ADE).
R là tâm phép vị tự quay biến C' thành B, B' thành C nên biến C'B thành B'C, mặt khác ta có:
$\frac{C'D}{BC'}=\frac{EB'}{CB'}$
Vậy biến D thành E.
DC' cắt EB' tại A nên tứ giác RDEA nội tiếp hay R thuộc (ADE)
Bài 3: Cho tam giác ABC nội tiếp (O). Đường tròn nội tiếp (I) tiếp xúc BC, CA, AB tại D, E, F. X là điểm chính giữa cung BC chứa A. (AIX) lần lượt cắt AB, AC tại Y, Z. (DYZ) cắt (I) tại W và D. Gọi M là trung điểm BC, P là tiếp điểm của đường tròn mixtilinear trong góc A. Chứng minh rằng:
a) BY=BM=CZ=CM
b) A, W, P thẳng hàng.
Lời giải:
Gọi N là giao điểm AI và (O).
a)Rõ ràng X, M, N thẳng hàng Phép vị tự quay tâm A. biến:
YB thành IN, nên: $BY=NI\cdot \frac{BX}{NX}=NB\cdot \frac{BX}{NX}=BM$ Tương tự CM=CZ.
b) Từ (1) suy ra Y, M đối xứng với nhau BI, Z, M đối xứng nhau qua CI suy ra I là tâm của (MYZ) và do:
YZ là trục đẳng phương (MYZ) và (YZDW) nên tâm của (YZDW) và I vuông góc YZ
Mặt khác có tâm của (YZDW) và I vuông WD ( WD là trục đẳng phương) nên:
WD song song YZ. Theo định lý Euler ta lại có:
$IP.IX=2rR=ID.XN$Suy ra tam giác IDP đồng dang tam giác XIN, và do XIN đồng dạng XZC (do phép vị tự quay tâm X) và IDP=IWP (Do D và W đối xứng) vậy:
tam giác IWP đồng dạng tam giác XZC.
$ \angle IPW= \angle XCA= \angle XPA$ nên P, W, A thẳng hàng.
Hay W và D đối xứng nhau qua IP
Bài 4: Cho tam giác ABC có (I) là tâm nội tiếp và các tiếp điểm D, E, F trên BC, CA, AB. đường thẳng qua D vuông EF cắt AB tại X. Gọi T là giao điểm của (ADE) và (ABC). Chứng minh rằng
a) TF vuông TX
b) Tâm đường tròn nội tiếp của tam giác TEF thuộc (I) (
thinhrost1)
Lời giải:
AI cắt (ABC) tại G, Gọi AA' là đường kính của (O). Theo kết quả quen thuộc T, I, A' thẳng hàng.
Phép vị tự quay tâm T biến B thành F, C thành E nên
tam giác TBF đồng dạng tam giác TCE nên :
BD/CD=BF/CE=TB/TC như vậy TD là phân giác của $\angle BTC$. Phép vị tự quay tâm T biến EF thành BC biến (TEF) thành (TBC) nên biến I thành G, mà T,D,G thẳng hàng nên gọi Y là giao TI và EF thì phép vị tự này biến Y thành D, do biến I thành G và TDG, TYI thẳng hàng nên YD song song IG hay YD vuông EF như vậy BF cắt DY tại X thì suy ra tứ giác TFXY nội tiếp suy ra: $ \angle XTF= 90^o$
b) Gọi J là tâm nội tiếp của TEF, K là tâm nội tiếp TBC. Thì phép vị tự quay tâm T biến J thành K. Biến TJ, FJ, EJ thành BK, TK, CK, nên $\ange FIE = \angle BJC$ mà $ \angle BJC=90^0+\angle T/2 =90^0+\angle A /2 = \angle FDE$ Vậy IDFE nội tiếp. ta có đpcm
















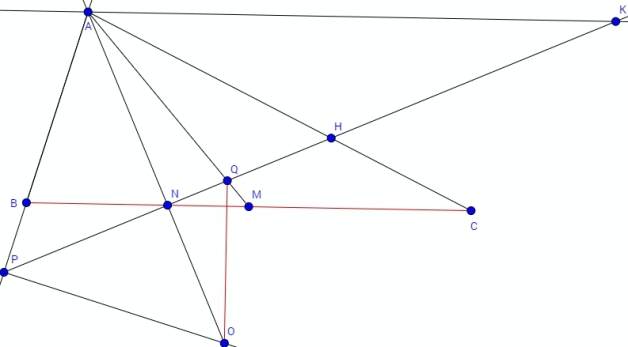





 . Ta có bổ đề
. Ta có bổ đề



 Vậy bổ đề được chứng minh
Vậy bổ đề được chứng minh




 .
.