Dùng tỉ số kép để chứng minh thẳng hàng

Cho tam giác ABC và E, F thuộc AC, AB. M, N thuộc BE, CF. FM cắt EN tại T. BN cắt CM tại S. Chứng minh A, S, T thẳng hàng.

Dùng biến đổi góc để chứng minh thẳng hàng

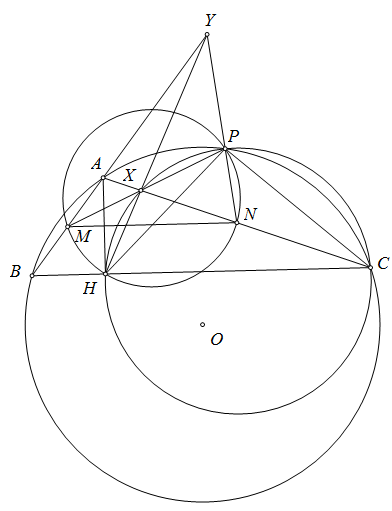
Bài: Cho $\Delta ABC$ tù ở $A$ nội tiếp $(O),$ có đường cao $AH$ và đường trung bình ứng với $BC$ là $MN(M \in AB).$

$(HMN)$ cắt $(O)$ ở $P.PM,PN$ cắt $AC,AB$ ở $X,Y.$ Chứng minh $XY$ đi qua $H.$

Lời giải:

Ta có $\angle HPM=\angle MNH=\angle MNA=\angle ACB\Longrightarrow P,X,H,C$ cùng thuộc một đường tròn

$\Longrightarrow \angle PHX=\angle PCA$. Tương tự thì $\angle PHY=\angle PBA\Longrightarrow \angle PHX=\angle PHY\Longrightarrow H,X,Y$ thẳng hàng hay $XY$ đi qua $H.\blacksquare$

Ứng dụng đường tròn điểm trong giải toán

Đề:
Cho tam giác ABC và điểm P. AP, BP, CP cắt BC, CA, AB tại D, E, F. Gọi Q là điểm đẳng giác của P trong tam giác DEF. Đường thẳng qua P vuông góc với AP, BP, CP cắt BC, CA, AB tại X, Y, Z. Chứng minh X, Y, Z cùng nằm trên đường thẳng d và D vuông góc với PQ

Lời giải:

Dùng tỉ số kép với các đường lần lượt vuông góc như sau:

$P(AXYZ)=P(XABC)=A(XPBC)=A(PXCB)=A(PXYZ)$

Vậy X, Y, Z thẳng hàng.

Ý sau chứng minh khó theo Huỳnh Bách Khoa:

Ở lời giải trên ta đã dùng bổ đề sau:

Từ bổ đề đường tròn tiếp xúc đến bài toán mở rộng Serbia 2016

$\boxed{\text{Bài toán}}$(Serbia 2016) Cho tam giác $ABC$ có đường cao $AH$ và tâm nội tiếp $I$. $IB,IC$ cắt $AH$ tại $M,N$. $K,L$ là tâm ngoại tiếp tam giác $MAB,NAC$. $R,Q$ là trung điểm $IB,IC$. Lấy $P$ sao cho $PR\perp NL,PQ\perp MK$. Một tiếp tuyến thay đổi của đường tròn Euler của tam giác $IBC$ cắt $PQ,PR$ tại $S,T$. $X$ đối xứng $P$ qua $S,T$. Chứng minh rằng đường tròn $(XST)$ luôn tiếp xúc một đường tròn cố định khi tiếp tuyến thay đổi.

Lời giải:

Ta cần có hai bổ đề sau:

$\boxed{\text{Bổ đề 1}}$ Cho tam giác $ABC$ có $O$ là tâm ngoại tiếp. Một đường tiếp tuyến với $\odot (BOC)$ cắt $AB$ ở $D$ và $CA$ ở $E$. Gọi $A'$ là điểm đối xứng của điểm $A$ qua $DE$. Khi đó $\odot (A'DE)$ tiếp xúc $\odot (ABC)$.

Chứng minh. Gọi $X$ là tiếp điểm $BX,CX$ cắt $\odot (O)$ tại $K,L.KE,LD$ cắt nhau tại $S$. Theo định lí $Pascal$ đảo thì $S$ thuộc $\odot (O)$


Biến đổi góc: $\angle DSE=\angle LCK=\angle BXC-\angle BKC=\angle BOC-\angle BAC=\angle BAC=\angle DA'E$

$\Longrightarrow D,S,A',E$ đồng viên.

Mặt khác: $\angle EXC=\angle KBC=\angle ESC$ nên $E,L,S,C$ đồng viên.

$\Longrightarrow E,X,S,C$ đồng viên.

$\Longrightarrow \angle DES=\angle XCS=\angle LKS$

$\Longrightarrow DE\parallel KL$

$\Longrightarrow \odot (DSE)$ tiếp xúc $\odot (DLK)$ hay $\odot (A'DE)$ tiếp xúc $\odot (ABC).\blacksquare$

$\boxed{\text{Bổ đề 2}}$ Cho tam giác $IBC.Q,R$ lần lượt là trung điểm $IC,IB$. Kí hiệu $\omega $ là đường tròn $Euler$ của $\triangle IBC.PR,PQ$ cắt $\omega $ tại $F,E$. Khi đó tâm $\odot (PEF)$ thuộc $\omega $.

Chứng minh. Gọi $I'$ là trung điểm $BC$.



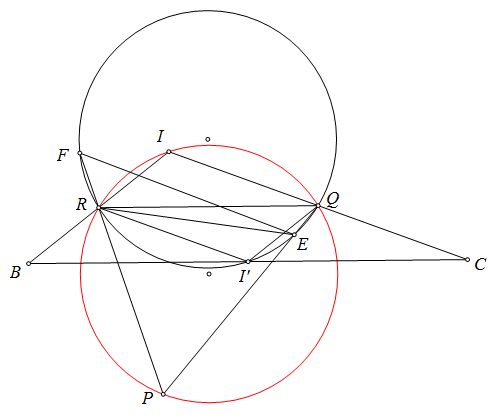
Ta có $\angle RPE=180^\circ-\angle RIQ=180^\circ-\angle RI'Q=180^\circ-\angle REQ=\angle REP$

$\Longrightarrow \angle FRE=2\angle FPE\Longrightarrow $ tâm $\odot (PEF)$ thuộc $\omega .\blacksquare$

Quay lại bài toán.

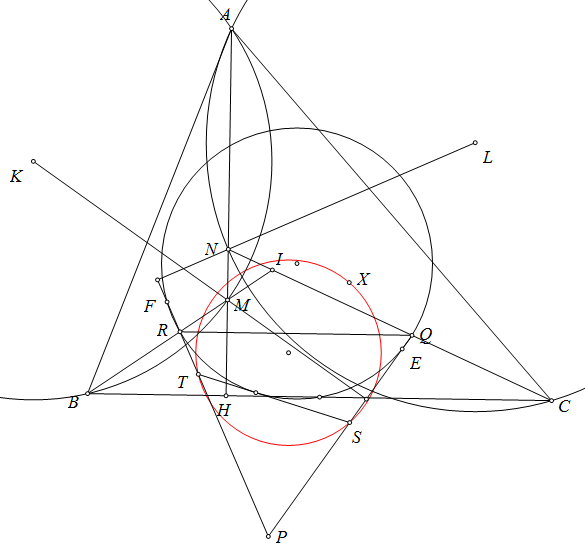
Ta có $\angle IQP=90^\circ-\angle IMN+\angle AMK=90^\circ-\angle B/2+\angle C/2$. Tương tự $\angle IRP=90^\circ-\angle C/2+\angle B/2$.

Gọi $E,F$ lần lượt là giao của $PQ,PR$ với đường tròn $Euler$ của tam giác $IBC$. Theo bổ đề $2$ ta suy ra tâm $\odot (PEF)$ thuộc đường tròn $Euler$ của tam giác $IBC$. Theo bổ đề $1$ ta suy ra $\odot (PEF)$ tiếp xúc $\odot (XST).\blacksquare$

Kết hợp giữa phép nghịch đảo và định lý Miquel

Bài 1: Cho tam giác ABC, đường tròn (K) qua B, C cắt AC, AB tại E, F. BE cắt CF tại H. Gọi Q là tâm đường tròn (HEF), L là tâm đường tròn KBC. Chứng minh rằng Q, K, L thẳng hàng.

Lời giải

Gọi S là giao của (ABE) và (ACF) theo định lý Miquel ta có S thuộc (BFH) và (HEC). Suy ra:

∠BSC=360°-∠BSH-∠HSC=∠BFC+∠BEC=∠BKC Suy ra tứ giác BSKC nội tiếp.

Xét phép nghịch đảo tâm A đối với (K), biến:

F thành B

E thành C
Suy ra EB thành (ABE), CF thành (ACF)

Nên biến H là giao điểm EB và FC thành S là giao điểm (ABE), (ACF)

Nên phép vị tự này biến (HEF) thành (BSC) nên tồn tại phép vị tự tâm A tỉ số k biến Q thành L.

Vậy A, Q, L thẳng hàng

Bài 2: (tiếng anh) Let $\triangle ABC$. A circle passes through $B,C$ intersects $AC,AB$ at $E,F$. The lines passes through $E,F$ and perpendicular to $AC,AB$ intersect together at $O. M,N$ lies on $EO,FO$,respectively. Draw $CQ\perp AM,BP\perp AN. BP$ and $AM$ intersects together at $I.MB$ intersect $NC$ at $K$.
Prove that $O,I,K$ are collinear.

Solution

Lemma: Let $ABCD$ is a quadrilateral. $AB$ cuts $CD$ at $G$; $AD$ cuts $BC$ at $K$. Then three circles with diameter $AC,BD,GK$ have the same radical axis.
Proof

Let $H,H'$ are the orthocenters of $\triangle GAD$ and $\triangle KCD$ respectively. Suppose that $GH,AH,DH$ cut $AD,GD,GA$ at $P,Q,R$ respectively. We have $HG.HP=HA.HQ=HD.HR$ so $H$ is on the radical axis of three circles with diameter $AC,BD,GK$. Similarly, we have $H'$ is on the radical axis of three circles with diameter $AC,BD,GK$, too. Hence, $HH'$ is the radical axis of three circles with diameter $AC,BD,GK$ so three cicles with diameter $AC,BD,GK$ have the same radical axis.
Back to this problem Let $X,Y,Z$ are the midpoints of $AO,AI,AK$ respectively. $BC$ cuts $MN$ at $G$. $H$ lies on $AK$ such that $GH \perp AK$. We have $AF.AB=AE.AC$ so $A$ lies on the radical axis of the circles with diameter $BN,CM$. According this lemma, we have $AH.AK=AF.AB=AE.AC$. The inversion center $A$, radius $AF.AB$ : $(X;XA) \mapsto BC; (Y;YA) \mapsto MN; (Z,ZA) \mapsto$ the line passing $H$ and perpendicular $AK$. But $BC, MN$ and the line passing $H$ and perpendicular $AK$ are concurrent at $G$. So $(X;XA), (Y;YA), (Z;ZA)$ have the same radical axis $\Longrightarrow$ $X,Y,Z$ are collinear. Hence $O,I,K$ are collinear.

Bài 3: Cho tam giác ABC. Đường tròn (O) đi qua B, C cắt AC, AB tại E, F. BE cắt CF tại D. H là hình chiếu của O trên AD. K, L là tâm (AFC) và (AEB). I là giao điểm khác H của (KHF) và (LHE). CMR: AI đi qua trung điểm BC.
Lời giải (Huỳnh Bách Khoa)

Lưu ý thêm:
Ta cần bổ đề sau: Gọi H là giao của (BDF) và (DEC). Thì OH vuông DH. Ta có thể gọi M, N là trung điểm FC, EB. Sau đó dùng vị tự quay để suy ra OHMND đồng viên đường tròn đường kính OD. (China 1992)

Và một số sai sót: M thuộc (LEH) do  ∠MLH=∠HEC

Phép gọi T là đối xứng D qua trung điểm BC thường hay gặp để tạo ra đường đẳng giác góc A với AH
Và còn ∠DHN=∠NAH=∠DXN
Về phần phép nghịch đảo là phương tích AE.AC, biến E thành C, F thành B. Thay điểm G thành D. Do I là giao của (MEH) và (NHF) nên biến thành Z là giao của (BDX) và (CDY)

Dùng đạo hàm để giải bất đẳng thức

Đề:

Cho a, b, c là các số thực không âm đôi một khác nhau

Tìm giá trị nhỏ nhất của biểu thức $P=\left [ (a+b)^{2}+(b+c)^{2}+(c+a)^{2} \right ]\left [ \frac{1}{(a-b)^{2}}+\frac{1}{(b-c)^{2}}+\frac{1}{(c-a)^{2}} \right ]$

Lời giải:

Giả sử $a > b > c \ge 0$
Khi đó $P= \Big[(a+b)^2+(b+c)^2+(c+a)^2 \Big].\left[ \frac{1}{(a-b)^2}+\frac{1}{(b-c)^2}+\frac{1}{(a-c)^2}\right]$
$\ge \left[ (a+b)^2 +a^2+b^2\right] .\left[ \frac{1}{(a-b)^2}+\frac{1}{a^2}+\frac{1}{b^2}\right]$
$=2\left[(a+b)^2-ab \right].\left[ \frac{1}{(a+b)^2-4ab}+\frac{(a+b)^2}{a^2b^2}-\frac{2}{ab}\right]$
BDT đã cho có dạng thuần nhất nên chuẩn hóa $a+b=1,$ đặt $ab=x,0< x \le \frac 14$
Khi đó $\frac F2 \ge(1-x)\left( \frac{1}{1-4x}+\frac{1}{x^2}-\frac 2x\right)$
$=3+\frac{1}{x^2}-\frac{3}{x}+\frac{3x}{1-4x}$
Khảo sát hàm số $f(x)=\frac{1}{x^2}-\frac{3}{x}+\frac{3x}{1-4x}$ trên $\left[0;\frac 14 \right)$
Ta thu được $\min f(x)=\frac{35+11\sqrt{33}}{8}$
Từ đó suy ra $F \ge \frac{59+11\sqrt{33}}{4}$
$\min F=\frac{59+11\sqrt{33}}{4}$ đạt được chẳng hạn khi $a,b$ là 2 nghiệm của pt $x^2-x+\frac{13-\sqrt{33}}{34},c=0$

Bài toán mở rộng về đường tròn chín điểm ( Tiếng Anh)

Let $ABC$ be a triangle with circumcircle $(O)$. $(K)$ is a circle passing through $B,C$. $(K)$ cuts $CA,AB$ again at $E,F$. $BE$ cuts $CF$ at $H_K$.

a) Prove that $H_KK$ and $AO$ intersect on $(O)$.

b) $O_K$ is isogonal conjugate of $H_K$ with respect to triangle $ABC$. Prove that $O_K$ lies on $OK$.

c) Let $L,N$ be the points on $CA,AB$, resp such that $O_KL\parallel BE, O_KN\parallel CF$. Prove that $LN\parallel BC$.

d) The line passing through $N$ parallel to $BE$ cuts the line passing through $L$ parallel to $CF$ at $P$. Prove that $P$ lies on $AH_K$.

e) $Q,R$ lie on $BE,CF$, resp such that $PQ\parallel AB,PR\parallel AC$. Prove that $QR\parallel BC$.

f) Prove that $NQ,LR$ and $AH_K$ are concurrent.

g) $D$ is projection of $K$ on $AH_K$. Prove that $DK,EF,BC$ are concurrent.

h) Prove that $KN\perp BE, KL\perp CF$.

i) Prove that nine points $D,E,F;P,Q,R;K,L,N$ lie on a circle $(N_K)$.

j) Prove that $N_K$ is midpoint of $PK$ and $KN_K$ is parallel to $AO$.

k) Prove that $H_K,N_K,O$ are collinear.

When $K \equiv M$ midpoint of $BC$, we get all properities of Nine-point circle.

Solution:

a, g) Let $S \equiv EF \cap BC.$ Then $AS$ is the polar of $H_K$ WRT $(K)$ and $AH_K$ is the polar of $S$ WRT $(K)$ $\Longrightarrow$ $KH_K$ is perpendicular to $AS$ through $H$ and $AH_K$ is perpendicular to $KS$ through $D.$ Hence $SH \cdot SA=SD \cdot SK=SB \cdot SC$ $\Longrightarrow$ $H \in (O).$ Since $\angle AHH_K=90^{\circ},$ then $KH_K$ and $AO$ meet on $(O).$

b, c) $\angle O_KBC=\angle H_KBF=\angle H_KCE=\angle O_KCB$ $\Longrightarrow$ $O_K$ is on perpendicular bisector $OK$ of $\overline{BC}.$ $\angle BFC=\angle BNO_K=\angle BKO_K$ (mod 180) $\Longrightarrow$ $N,B,K,O_K$ are concyclic $\Longrightarrow$ $\angle BNK=\angle BO_KK.$ But $\angle BO_KK=90^{\circ}-\angle FBE=\angle FEK$ $\Longrightarrow$ $\angle BNK=\angle FEK,$ i.e. $N$ lies on circumcircle $(N_K)$ of $DKEF.$ Similarly, $L \in (N_K).$ Thus, $LN$ is antiparallel to $EF$ WRT $AE,AF$ $\Longrightarrow$ $LN \parallel BC.$

d, f)$\triangle PLN$ and $\triangle H_KCB,$ with parallel sides, are homothetic with center $A$ $\Longrightarrow$ $A,P,H_K$ are collinear. Likewise, $\triangle ANL$ and $\triangle PQR,$ with parallel sides, are homothetic with center $AP \cap NQ \cap LR,$ i.e. $AH_K,NQ,LR$ concur.

i) $\angle NKL=\angle NBO_K+\angle LCO_K=CBH_K+\angle BCH_K=\angle NPL$ (mod 180) $\Longrightarrow$ $P \in (N_K).$ Further, $P$ is the midpoint of the arc $EF$ of $(N_K),$ because $\angle PFK=\angle PDK=90^{\circ},$ i.e. $KP$ is perpendicular bisector of  $\overline{EF}.$ Now, since $\angle PQE=\angle FBE=\angle PKE,$ it follows that $Q \in (N_K).$ Similarly, $R \in (N_K).$

h, j) $D,E,F,P,Q,R,K,L,N$ lie then on a circle $(N_K)$ with diameter $KP$ perpendicular to $EF,$ i.e. $KP \parallel AO.$ Thus, $KN$ is perpendicular to $PN \parallel BE$ and $KL$ is perpendicular to $PL \parallel CF.$

e, k) $\triangle PQR \cup (N_K)$ and  $\triangle ABC \cup (O)$ are homothetic with center $H_K \equiv AP \cap BQ \cap CR,$ thus $QR \parallel BC$ and $H_K,O,N_K$ are collinear.

Dùng pqr để chứng minh bất đẳng thức

Bài 1:

Cho ba số thực

a⩾b⩾1⩾c⩾0a⩾b⩾1⩾c⩾0 thỏa mãn điều kiện a+b+c=3.
 Chứng minh rằng
 $\frac{24}{a^3+b^3+c^3} + \frac{25}{ab+bc+ca} \geqslant 14.$ Đẳng thức xảy ra khi nào ?

Lời giải:



Đặt $q=ab+bc+ca, r=abc.$

$1.$ Vì $(1-a)(1-b)(1-c)=q-r-2\geq 0$ nên $q\geq r+2\geq 2.$

Lại có $3(ab+bc+ca)\leq (a+b+c)^2$ nên $ab+bc+ca\leq 3.$

$2.$ Bất đẳng thức tương đương

$$\frac{8}{9-3q+r}+\frac{25}{q}\geq 14$$

mà ta lại có $r\leq q-2$ nên ta chỉ cần chứng minh

$$\frac{8}{7-2q}+\frac{25}{q}\geq 14$$

$$\Leftrightarrow 7(2q-5)^2\geq 0.$$

Đẳng thức xảy ra khi và chỉ khi $a=\frac{2+\sqrt{2}}{2}, b=1, c=\frac{2-\sqrt{2}}{2}.$

Bài 2:

$x,y,z >0$ và $x^2+y^2+z^2=3$.CMR: $\sum \frac{1}{7-xy} \leq \frac{1}{2}$

Lời giải:

Bất đẳng thức tương đương
\[294-28(xy+yz+xz)+2xyz(x+y+z)\leq 343-49(xy+yz+xz)+7xyz(x+y+z)-(xyz)^2\]
\[\Leftrightarrow 21(xy+yz+xz)+(xyz)^2\leq 49+5xyz(x+y+z)\]
Đặt $x+y+z=p,xy+yz+xz=q,xyz=r$ và $p^2-2q=3$, Ta cần chứng minh
\[21q+r^2\leq 49+ 5pr\]
Vì $r^2\leq 1$ Ta sẽ chứng minh bất đẳng thức mạnh hơn
\[21q\leq 48+5pr\]
Theo bất đẳng thức Schur bậc 3, $r\geq \frac{p(4q-p^2)}{9}=\frac{p(2q-3)}{9}$, Ta cần chứng minh rằng
\[21q\leq 48+\frac{5p^2(2q-3)}{9}=\frac{20q^2-45}{9}\]
\[\Leftrightarrow (q-3)(q-\frac{129}{20})\geq 0 \ \text{(Luôn đúng)} \ q\leq 3\].
Dấu bằng xảy ra khi và chỉ khi $a=b=c=1$.

Từ đẳng thức cho đến bất đẳng thức

Ta có đẳng thức sau:


Cho $xyz=1$ thì khi đó:

$\sum \frac{1}{xy+x+1}=1$

Ứng dụng:

Bài 1; (APMO 2016)


Cho ba số dương x,y,zx,y,z thỏa mãn điều kiện xyz=1. Chứng minh rằng

$\frac{1}{(x+1)^2+y^2+1} + \frac{1}{(y+1)^2+z^2+1} + \frac{1}{(z+1)^2+x^2+1} \leqslant {\frac{1}{2}}.$

Lời giải:

Áp dụng $AM-GM:$

$$\sum \frac{1}{(x+1)^2+y^2+1}=\sum \frac{1}{x^2+2x+1+y^2+1}\leq \frac{1}{2}\sum \frac{1}{xy+x+1}=\frac{1}{2}(\text{do }xyz=1)$$

Đẳng thức xảy ra khi $x=y=z=1.$

Bài 2 (Romanian JBMO TST 2016). Với a,b,ca,b,c là ba số thực dương thỏa mãn điều kiện abc⩾1. Chứng minh rằng:

$\dfrac{1}{a^3+2b^3+6}+\dfrac{1}{b^3+2c^3+6}+\dfrac{1}{c^3+2a^3+6} \le \dfrac{1}{3}.$

Lời giải:

Vì $abc \geq 1$ nên tồn tại $k \geq 1$ và $a',b',c'>0$ sao cho $a=ka', b=kb', c=kc'$ và $a'b'c'=1$.

Suy ra $a\geq a', b\geq b', c\geq c'$.

Do đó
\[\sum_{a,b,c}\frac{1}{a^3+2b^3+6}\leq \sum_{a',b',c'}\frac{1}{a'^3+2b'^3+6}=\sum_{a',b',c'}\frac{1}{(a'^3+b'^3+1)+(b'^3+1+1)+3}\leq \frac{1}{3}\sum_{a',b',c'}\frac{1}{a'b'+b'+1}=\frac{1}{3}.\]
Ta có đpcm.

Ứng dụng bất đẳng thức Bernoulli

 Cho $n$ số thực dương  $a_1,a_2,\dots ,a_n.$ Chứng minh rằng;

$\prod_{i=1}^{n} \left(1+\frac{1}{a_i}\right)^{a_{i+1}-a_i} \geqslant 1,$

Lời giải:





Áp dụng BĐT $Bernoulli,$ ta có:

$$\left(1+\frac{1}{a_i}\right)^{a_{i+1}-a_i}\geq 1+\frac{a_{i+1}-a_i}{a_i}=\frac{a_{i+1}}{a_i}$$

Do đó:

$$\prod_{i=1}^{n} \left(1+\frac{1}{a_i}\right)^{a_{i+1}-a_i}\geq \frac{a_2}{a_1}.\frac{a_3}{a_2}\cdots \frac{a_1}{a_n}=1$$

Đánh giá từng số hạng trong bất đẳng thức

Đề: Cho ba số thực dương a,b,ca,b,c thỏa mãn điều kiện a+b+c=3. Chứng minh rằng


$\frac{a^3+b^3}{a^2+ab+b^2}+\frac{b^3+c^3}{b^2+bc+c^2}+\frac{c^3+a^3}{c^2+ca+a^2} \geqslant 2.$

Lời giải:

Ta có:

$$\frac{a^2-ab+b^2}{a^2+ab+b^2}\geq \frac{1}{3}\Leftrightarrow \frac{2(a-b)^2}{3(a^2+ab+b^2)}\geq 0,\text{đúng}$$

Do đó:

$$\sum \frac{a^3+b^3}{a^2+ab+b^2}=\sum (a+b).\frac{a^2-ab+b^2}{a^2+ab+b^2}\geq \sum \frac{1}{3}(a+b)=2$$

Đẳng thức xảy ra khi $a=b=c=1$

Đặt ẩn phụ trong chứng minh bất đẳng thức

Đề bài: Cho ba số thực dương 
$a,b,c$ thỏa mãn $a+b+c=3.$ Chứng minh rằng
$\sqrt{\frac{b}{a^2+3}}+\sqrt{\frac{c}{b^2+3}}+\sqrt{\frac{a}{c^2+3}} \leqslant \frac32\sqrt[4]{\frac{1}{abc}}.$

Lời giải

Ta sẽ cố gắng đưa về bất đẳng thức đồng bậc

Vế phải của bất đẳng thức thực ra là $\dfrac{1}{2}.\dfrac{3}{\sqrt[4]{abc}}=\dfrac{a+b+c}{2\sqrt[4]{abc}}$

Áp dụng bất đẳng thức AM-GM thì $a^2+3\geq 4\sqrt{a}$ nên $VT\leq \sum \dfrac{\sqrt{b}}{2\sqrt[4]{a}}$

Đặt $\sqrt[4]{a}=x,\cdots $ thì ta chỉ cần chứng minh $\sum \dfrac{y^2}{x}\leq \dfrac{x^4+y^4+z^4}{xyz}\Leftrightarrow x^3y+y^3z+z^3x\leq x^4+y^4+z^4$

Bất đẳng thức trên chứng minh khá dễ bằng AM-GM

Điểm rơi trong bất đẳng thức Cauchy

(Saudi Arabia TST 2016). Cho ba số thực dương $a,b,c$ thỏa mãn điều kiện $a+b+c=3.$ Chứng minh rằng:
$\frac{1}{a^2+b^2+c^2}+\frac{1}{\sqrt{abc}} \geqslant \frac{4}{3}.$
Lời giải:

Đặt $t=ab+bc+ca$, với $t \in (0;3]$.
Sử dụng liên tiếp AM-GM ta có $3^6 = [a^2+b^2+c^2+2(ab+bc+ca)]^3 \geq 27(a^2+b^2+c^2)(ab+bc+ca)^2$ $\Leftrightarrow$ $\frac{1}{a^2+b^2+c^2} \geq \frac{t^2}{27}$. Mặt khác $3 \geq t \geq 3 \sqrt[3]{a^2b^2c^2}$. Do đó $\frac{1}{\sqrt{abc}} \geq \sqrt{\dfrac{27}{t^3}}$. Từ đó ta có $\frac{1}{a^2+b^2+c^2} + \frac{1}{\sqrt{abc}} \geq \frac{t^2}{27} + \sqrt{\frac{27}{t^3}} = \frac{t^2}{81}.3 + \frac{1}{9}\sqrt{\frac{27}{t^3}}.4 + \dfrac{5}{9}\sqrt{\frac{27}{t^3}} \geq 7\sqrt[7]{(\frac{t^2}{81})^3.(\dfrac{1}{9}\sqrt{\frac{27}{t^3}})^4} + \frac{5}{9} = \frac{4}{3}$. Dấu bằng xảy ra khi $a=b=c=1$.

Phương pháp sắp thứ tự các biến trong bất đẳng thức

Bài (Russia 2016): Cho bốn số thực dương $a,b,c,d$ thỏa mãn điều kiện $a+b+c+d=3.$ Chứng minh rằng:



a) $\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+\frac{1}{d^2}\le\frac{1}{a^2b^2c^2d^2},$




b) $\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}+\frac{1}{d^3}\le\frac{1}{a^3b^3c^3d^3}.$


Lời giải

$(a)$ Giả sử $a \geqslant b \geqslant c \geqslant d$, BĐT cần chứng minh tương đương với

$a^{2}b^{2}c^{2}+a^{2}b^{2}d^{2}+a^{2}c^{2}d^{2}+b^{2}c^{2}d^{2} \leqslant 1$

Ta đưa BĐT về dạng đồng bậc

$a^{2}b^{2}c^{2}+a^{2}b^{2}d^{2}+a^{2}c^{2}d^{2}+b^{2}c^{2}d^{2} \leqslant \frac{1}{3^6}(a+b+c)^6$

Do $a \geqslant b \geqslant c \geqslant d$ nên ta có

\[\begin{aligned} a^{2}b^{2}c^{2}+a^{2}b^{2}d^{2}+a^{2}c^{2}d^{2}+b^{2}c^{2}d^{2} &\leqslant a^{2}b^{2}c^{2}+a^{2}b^{2}d^{2}+a^{2}b^{2}cd+a^{2}b^{2}cd \\ &= a^{2}b^{2}(c+d)^{2} \\ &\leqslant \frac{1}{3^{6}}(a+b+c+d)^{6} \\ &=1\end{aligned}\]

Bài toán được chứng minh. $\square$

$(b)$ Giả sử $a \geqslant b \geqslant c \geqslant d$, BĐT cần chứng minh tương đương với

$a^{3}b^{3}c^{3}+a^{3}b^{3}d^{3}+a^{3}c^{3}d^{3}+b^{3}c^{3}d^{3} \leqslant 1$

Ta đưa BĐT về dạng đồng bậc

$a^{3}b^{3}c^{3}+a^{3}b^{3}d^{3}+a^{3}c^{3}d^{3}+b^{3}c^{3}d^{3} \leqslant \frac{1}{3^9}(a+b+c)^9$

Theo BĐT $AM - GM$ ta có

$ \frac{1}{3^9}(a+b+c+d)^9 \geqslant \frac{1}{3^9}\left(3\sqrt[3]{ab(c+d)} \right)^9 = a^3b^3(c+d)^3 $

Do đó ta chỉ cần chứng minh $a^{3}b^{3}c^{3}+a^{3}b^{3}d^{3}+a^{3}c^{3}d^{3}+b^{3}c^{3}d^{3} \leqslant a^3b^3(c+d)^3$ $\Leftrightarrow c^3d^3(a^3+b^3) \leqslant 3a^3b^3cd(c+d)$ $\Leftrightarrow c^2d^2(a^3+b^3) \leqslant 3a^3b^3(c+d)$

BĐT này luôn đúng do $a \geqslant b \geqslant c \geqslant d$

Bài toán được chứng minh. $\square$$

Bất đẳng thức với số thực

Đề bài: Cho ba số thực $a,b,c$ thỏa mãn điều kiện $a^2+b^2+c^2=4+abc.$ Chứng minh rằng


$(a^2+2)(b^2+2)(c^2+2)\ge 9+6(ab+bc+ca).$

Lời giải:

Áp dụng bất đẳng thức AM-GM ta có $a^2+b^2+c^2=4+abc\geq 3\sqrt[3]{a^2b^2c^2}$

Đặt $\sqrt[3]{abc}=t\Rightarrow t^3+4\geq 3t^2\Leftrightarrow (t+1)(t-2)^2\geq 0\Leftrightarrow t\geq -1\Rightarrow abc\geq -1\Rightarrow a^2+b^2+c^2\geq 3$.

Ta sẽ chứng minh $3(a+b+c)^2\leq (a^2+2)(b^2+2)(c^2+2)$.

Ta có $(a+b+c)^2=(a.1+\sqrt{2}.\frac{b+c}{\sqrt{2}})^2\leq (a^2+2)(1+\frac{(b+c)^2}{2})$.

Do đó ta chỉ cần chứng minh $(b^2+2)(c^2+2)\geq 3(1+\frac{(b+c)^2}{2})\Leftrightarrow (bc-1)^2+\frac{(b-c)^2}{2}\geq 0$ ( luôn đúng)

Vậy $(a^2+2)(b^2+2)(c^2+2)\geq 3(a+b+c)^2=3(a^2+b^2+c^2)+6(ab+bc+ca)\geq 9+6(ab+bc+ca)$ ( do $a^2+b^2+c^2\geq 3$).

Vậy ta có đpcm.

Nhận xét: Ở đây ta đã sử dụng bổ đề rất quen thuộc đó là: $3(a+b+c)^2\leq (a^2+2)(b^2+2)(c^2+2)$.

Phương pháp uct trong bất đẳng thức

Bài 1: (Iran TST 2016): Cho bốn số thực dương 
$a,b,c,d$ thỏa mãn điều kiện $\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}+\frac{1}{d+1}=2.$

Chứng minh: $\sqrt{\frac{a^2+1}{2}} +\sqrt{\frac{b^2+1}{2}}+\sqrt{\frac{c^2+1}
{2}}+\sqrt{\frac{d^2+1}{2}} +8 \geqslant 3(\sqrt{a}+\sqrt{b}+\sqrt{c}+\sqrt{d}).$

Lời giải:

Ta thấy có thể tách a,b ,c không ràng buộc với nhau và có thể đánh giá từng vế, nên ta cần tìm x và y sao cho:

$\sqrt{\frac{a^2+1}{2}} - 3\sqrt{a} \ge \frac{x}{a+1}+y$ (1)

Tương tự với b,c ta được: $2x+4y=-8$

Ngoài ra dấu bằng của $(1)$ xảy ra  khi $a=b=c=d=1$ thay vào trên ta lại có hệ:

$f'(a)=0$ với $f(a)=\sqrt{\frac{a^2+1}{2}} - 3\sqrt{a} -\frac{x}{a+1}$

Giải được $x=-y=4$

ta sẽ cm $\sqrt{\frac{a^{2}+1}{2}}-3\sqrt{a}\geq \frac{4}{a+1}-4$

$\Leftrightarrow \frac{(a+1)(a-1)^{2}}{2(\sqrt{\frac{a^{2}+1}{2}}+\sqrt{a})}-2\sqrt{a}(\sqrt{a}-1)^{2}\geq 0$

do $\sqrt{\frac{a^{2}+1}{2}}+\sqrt{a}\leq a+1$

nên ta cần cm $(\sqrt{a}-1)^{2}(\frac{(\sqrt{a}+1)^{2}}{2}-2\sqrt{a})\geq 0$(luôn đúng)

thiết lập các bất đẳng thức tương tự ta có đpcm

Bài 2: (Austrian 2016). Cho ba số thực 

$a,b,c⩾-1$ thỏa mãn điều kiện $a^3+b^3+c^3=1.$ Chứng minh rằng$$a+b+c+a^2+b^2+c^2⩽4.$$

Đẳng thức xảy ra khi nào ?

Lời giải:

Sử dụng bất đẳng thức $a^2+a-a^3-1\leq 0\Leftrightarrow (a+1)(a-1)^2\geq 0$

Xây dựng các bất đẳng thức tượng tự rồi cộng lại ta có đpcm.

Đẳng thức xảy ra khi và chỉ khi $(a,b,c)=(1,1,-1)$ và các hoán vị.

Dùng cô si ngược dấu để chứng minh bất đẳng thức

Đề:Với 
$a,b,c$ là ba số thực dương thỏa mãn $a+b+c=3.$ Chứng minh rằng:

$\frac{a^2}{a+b^2}+\frac{b^2}{b+c^2}+\frac{c^2}{c+a^2} \geqslant \frac{3}{2}$

Lời giải

Áp dụng AM-GM ta có:

$a-\frac{a^{2}}{a+b^{2}}=\frac{ab^{2}}{a+b^{2}}\leq \frac{ab^{2}}{2b\sqrt{a}}=\frac{b\sqrt{a}}{2}$

Tương tự cộng lại ta được:

$\sum \frac{a}{a+b^{2}}\geq 3-\frac{1}{2}(b\sqrt{a}+c\sqrt{b}+a\sqrt{c})\geq 3-\frac{1}{2}.\sqrt{(a+b+c)(ab+bc+ca)}\geq 3-\frac{1}{2}.\sqrt{(a+b+c).\frac{(a+b+c)^{2}}{3}}=3-\frac{3}{2}=\frac{3}{2}$

Dấu = xảy ra$\Leftrightarrow a=b=c=1$$