Dùng nguyên lí Dirichlet để giải bài toán tổ hợp - Phần 2

Bài toán: Tìm số tự nhiên n lớn nhát sao cho tồn tại n số nguyên không âm $x_1,x_2,..x_n$ không đồng thời bằng 0, sao cho với mọi $\varepsilon _1, \varepsilon _2,..\varepsilon _n$ $\in$ {-1;0;1} không đồng thời bằng 0 sao cho $n^3$ không chia hết cho $\varepsilon _1x_1+\varepsilon _2x_2+..\varepsilon _nx_n$

Lời giải.

Với n=9 ta chọn $1,2,2^2,..2^8$

Khi đó: $| \varepsilon _1+..+2^9\varepsilon _9|\le 1+2+..2^8<9^3$

Nếu $n\ge10$ không mất tính tổng quát, giả sử $n=10$ khi đó số tập con của S={$x_1,x_2,..z_10$} là $2^{10}$ và vì $2^{10}>10^3$ nên theo nguyên lí Dirichlet tồn tại hai tập A và B là tập con của S sao cho tổng các phần tử của A có cùng số dư với tổng các phần tử của B.

Khi đó đặt $\varepsilon _i=1$ nếu $x_i$ thuộc A nhưng không thuộc B, $\varepsilon _i=-1$ nếu $x_i$ thuôc B nhưng không thuộc A, bằng 0 trong trường hợp còn lại khi đó:

$\sum \varepsilon _ix_i \vdots n^3$

Dùng nguyên lí Dirichlet để giải bài toán tổ hợp-Phần 1

Bài toán: Gọi $n_1<n_2<..<n_{2000}<10^{100}$ là một số nguyên dương. Chứng minh rằng có thể tìm được hai tập A và B khác nhau không rỗng là tập con của {$n_1,n_2,..n_{2000}$} thỏa cấc điều kiện:

i) $|A|=|B|$

ii) $\sum_{x\in A}x=\sum_{x\in B}x$

iii) $\sum_{x\in A}x^2=\sum_{x\in B}x^2$

Lời giải

Lưu ý: $\binom{2000}{1000}$ là số hạng lớn nhất trong các số hạng $\binom{2000}{k}$.

Gọi S là tất cả tập con của tập {$n_1,n_2,..n_{2000}$} sao cho S có 1000 phần tử, ta có:

$0< \sum_{x\in S}x<1000.10^{100}$

$0< \sum_{x\in S}x^2<1000.10^{200}$

Vậy số các cặp $( \sum_{x\in S}x, \sum_{x\in S}x^2)$ ít hơn $10^{306}$

Mặt khác:

Số tập hợp chứa 1000 phần tử là: $\binom{2000}{1000}>\frac{\sum_{k=0}^{2000}\binom{2000}{k}}{2001}> \frac{2^{2000}}{2001}> \frac{10^{600}}{2001}>10^{306}$ 

Nên theo nguyên lí Dirichlet tồn tại hai tập hợp C và D chứa 1000 phần tử sao cho $( \sum_{x\in C}x, \sum_{x\in C}x^2)=( \sum_{x\in D}x, \sum_{x\in D}x^2)$

Loại bỏ các phần tử chung của C và D ta thu được hai tập A và B thỏa mãn điều kiện đề bài.

Bài toán của Gergone

Bài toán: Chứng minh rằng nếu một tứ giác có các đường thẳng nối trung điểm các cạnh đối đi qua giao điểm hai đường chéo thì tứ giác đó là hình bình hành.

Lời giải

https://drive.google.com/file/d/0BzFs5zQOA7paWXBCb0JTUGw5VTA/view?usp=sharing

Giải hệ phương trình bằng phương pháp UCT

1: Giải hệ phương trình sau:

$$\left\{\begin{matrix}
x^3+y^2=(x-y)(xy-1) & \\
x^3-x^2+y+1=xy(x-y+1) &
\end{matrix}\right.$$

Lời giải.

Ta thấy bậc y ở cả hai phương trình đều có bậc 2 nên ta sẽ biểu diễn theo y:

$\left\{\begin{matrix}
y^2(x+1)-y(x^2+1)+x^3+x=0 & \\
y^2x-y(x^2+x-1)+x^3-x^2+1=0 &
\end{matrix}\right.$

Ta cần tìm x để khi thay vào ta được hai phương trình tương đương. Tức là hệ số của chúng tỉ lệ;

$\frac{x+1}{x}=\frac{x^2+1}{x^2+x-1}=\frac{x^3+x}{x^3-x^2+1}\Leftrightarrow x=1$

Khi thay x=1 vào các hệ trên:

$\left\{\begin{matrix}
2(y^2-y+1)=0 & \\
(y^2-y+1)=0  &
\end{matrix}\right.$

Suy ra: 2PT(2)-PT(1) sẽ có nhân tử x-1:

$(x-1)(y^2-(x+3)y+x^2-x-2)=0$

Trường hợp x=1, phương trình vô nghiệm

Trường hợp x khác 1, ta được hệ mới:

$\left\{\begin{matrix}
y^2-(x+3)y+x^2-x-2=0 & \\
y^2(x+1)-y(x^2+1)+x^3+x=0  &
\end{matrix}\right.$

Tương tự ta được $x=\frac{-1}{2}$

Thay nó vào hệ ta rút ra được:

$2PT(2)-PT(1)=(2x+1)(y^2-(x-1)y+x^2-x+2)=0$

Xét trường hợp $x=\frac{-1}{2}$
...
Xét trường hợp x khác $\frac{-1}{2}$

Ta được hệ phương trình:

$\left\{\begin{matrix}
y^2-(x-1)y+x^2-x+2=0 & \\
y^2-(x+3)y+x^2-x-2=0 &
\end{matrix}\right.$

Trừ hai vế cho nhau ta có $y=-1$

Phần còn lại dành cho bạn đọc

Tương tự ta cũng có hệ sau:

$\left\{\begin{matrix}
2(x+y)(25-xy)=4x^2+17y^2+105& \\
x^2+y^2+2x-2y=7 &
\end{matrix}\right.$

Tương tự, nếu ta biểu diễn theo x ta sẽ không tìm được y, nhưng nếu biểu diễn theo y ta tìm được $x=2$, thay $x=2$ vào hệ:

$\left\{\begin{matrix}
21(y^2-2y+1)=0& \\
(y^2-2y+1)=0 &
\end{matrix}\right.$ nên PT(1)-21PT(2)=$(x-2)(2y^2+2xy+4y-17x-126)=0$

Trường hợp x=2 đơn giản, ta xét trường hợp x khác 2:

$\left\{\begin{matrix}
2y^2+2xy+4y-17x-126=0& \\
x^2+y^2+2x-2y-7=0 &
\end{matrix}\right.$

Đến đây phương trình vô nghiệm theo phương pháp uct $3PT(2)-PT(1)=(x-y+5)^2+2x^2+x+80=0$

Bất đẳng thức với số thực

Đề : Chứng minh với mọi a,b, c thực:

$ \sum a^6+a^2b^2c^2 \ge \frac{2}{3}(\sum a^5(b+c))$

Lời giải:

Áp dụng bất đẳng thức Schur ta có:

$ \sum a^6+3a^2b^2c^2 \ge \sum a^4(b^2+c^2)$

Theo AM-GM:

$(a^6+a^4b^2)+(a^6+a^4c^2) \ge 2 a^5(b+c)$

Tương tự cho b,c rồi cộng $4$ vế, ta có đpcm

Xây dựng tập hợp thỏa mãn đề bài

Đề: Chứng minh rằng tồn tại một tập A gồm vô hạn phần tử sao cho ta có thể trích tập hữu hạn B từ A, mà tổng các phần tử của B không phải là lũy thừa của một số nguyên

( Kvant)

Lời giải:

Xét tập hợp: A={$p^n.q^{n+1}: (p,q)=1, n \ge 1$}

Nếu B={$p^{n_1}.q^{n_1+1},...p^{n_k}.q^{n_k+1}$} là một tập hữu hạn trích từ A và $n_1<..n_k$

như vậy tổng các phần tử của B bằng: $p^{n_1}.q^{n_1+1}(1+p^{n_2-n_1}q^{n_2-n_1}+..)=p^{n_1}.q^{n_1+1}.N$

Mà $(N,p)=(N,q)=1$ nên ta có đpcm

Trường hợp nhỏ của định lý nổi tiếng của Erdos và Selfridge

Một định lý nổi tiếng của Erdos và Selfridge, một giả thuyết hơn 150 năm, nói rằng: Tích các số tự nhiên liên tiếp không thể là lũy thừa của một số nguyên.

Ta xét trường hợp tích 3 số tự nhiên liên tiếp.

Gọi n là số nguyên, và ta viết bài toán lại:

$n(n+1)(n+2)=x^z(x,z \in N, z \ge 2)$

Chú ý rằng: $n(n+2)=(n+1)^2-1$

Nên:

$\left\{\begin{matrix}
n+1=a^z & \\
(n+1)^2-1=b^z &
\end{matrix}\right.(a,b)=1\Rightarrow a^{2z}-b^z=1\Rightarrow (a^2-b)(..)=1\Rightarrow a^2=b+1\\\Rightarrow (b+1)^z-b^z=1 \Rightarrow z=1$

Vậy không tồn tại z thỏa mãn đề bài hay ta đã cm cho trường hợp $n=3$

Dùng bước nhảy Vi-et để giải bài toán

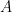Bài toán : Cho các số nguyên dương  thỏa mãn hệ thức  . Chứng minh rằng  là lũy thừa bậc năm của một số nguyên.

Lời giải :

Gọi 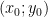 là cặp số thỏa mãn đề bài và có tổng  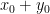nhỏ nhất. Ta giả sử .

Xét phương trình bậc hai ẩn  :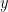

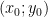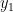Vì  thỏa mãn đề bài nên  là một nghiệm của phương trình . Gọi nghiệm còn lại là . Theo định lí  :

Ta có  nên từ 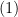 suy ra .

Các cặp  đều thỏa mãn  mà 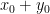 nhỏ nhất nên :

.

Như vậy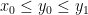 

• Trường hợp 1 :   thay vào  thì 
• Trường hợp 2 :  thì từ  ta được :

Dễ thấy  cùng tính chẵn lẻ mà 

Trường hợp này không xảy ra

• Trường hợp 3 : 

Suy ra 

Do đó từ 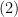 suy ra 

Khi  thì từ 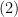 suy ra , vì . Vô lí vì phải có .

Tương tự khi xét . Tất cả đều dẫn đến vô lí. Trường hợp này loại.

Do đó ta luôn có 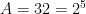 là lũy thừa bậc năm của một số nguyên. Đây là điều phải chứng minh.

Bài toán về "số chính phương tự do"

Ta định nghĩa: số nguyên dương n là "số chính phương tự do" - "square-free" khi n không có dạng $n=mp^2$ với m là số nguyên dương nào đó, $p$ là số nguyên tố.

Bài toán: (India MO 1995). Gọi n là số nguyên không âm sao cho n là ước của tổng:

$1+\sum_{i=1}^{n-1}i^{n-1}$.

Chứng minh rằng: n là một số chính phương tự do.

Lời giải:

Giả sử $n=mp^2$ khi đó:

$1+\sum_{i=1}^{n-1}i^{n-1}=1+\sum_{j=0}^{p-1}\sum_{k=0}^{mp-1}(kp+j)^{n-1}\equiv1+mp(\sum_{j=0}^{p-1}j^{n-1})\equiv1(mod p)$

Suy ra tổng đó không chia hết cho $p$, mâu thuẫn với đề bài. Vậy ta có đpcm

Chứng minh các bất đẳng thức không thuần nhất bằng Cauchy-Schwarz

1) Cho các số thực dương a,b,c chứng minh rằng:

$(a^2+2)(b^2+2)(c^2+2)\ge3 (a+b+c)^2$

Lời giải:

Theo bất đẳng thức Cauchy-Schwarz:

$(a+b+c)^2\le(a^2+2)(1+(b+c)^2/2)$

Như vậy ta chỉ cần chứng minh:

$(b^2+2)(c^2+2) \ge 3[1+(b+c)^2/2]$

Tương đương:

$(bc-1)^2+(b-c)^2/2 \ge 0$

Vậy ta có điều phải chứng minh.

Nhận xét:
bất
Ta có thể chắc chắn làm cách này là do tín độc lập của 3 biến a,b,c nên có thể xảy ra đẳng thức khi $a=2/(b+c)$ (điểm rơi C-S) Vì nếu nó đúng với mọi a,b,c thì cũng phải đúng với điểm a như thế.

2) Chứng minh bất đẳng thức sau đúng với mọi số thực a,b,c bất kì:

$(a^2+1)(b^2+1)(c^2+1) \ge (ab+bc+ca-1)^2$ (Indo TST 2007)

Lời giải:

$VP=(a(b+c)+(bc-1)^2]^2\le(a^2+1)((b+c)^2+(bc-1)^2)$

Mà $(b+c)^2+(bc-1)^2=(b^2+1)(c^2+1)$

Vậy ta có đpcm. Dấu bằng xảy ra khi $a+b+c=abc$

3) Cho các số thực a,b,c,d thỏa mãn:

$\prod (a^2+1)=16$

Chứng minh bất đẳng thức:
$-3 \le ab+ac+ad+bc+bd+cd-abcd \le 5$ (Titu Andreescu, Gabriel Dospinescu)

Lời giải:
BDT tương đương:

$( \sum ab-abcd-1)^2\le 16$

Dùng C-S:

$[a(b+c+d-bcd)+(bc+cd+db-1)^2] \le (a^2+1)[(b+c+d-bcd)^2+( bc+cd+db-1)^2]$

Mà: $(b+c+d-bcd)^2+( bc+cd+db-1)^2=(b^2+1)(c^2+1)(d^2+1)$

Ta có đpcm.

4) Chứng minh rằng với mọi a,b,c dương ta đều có:

$ \sum \sqrt{a(b+1)} \le \frac{3}{2}\sqrt{\prod (a+1)}$

Từ VT ta sẽ dùng C-S cho $\sqrt{ (a+1)} $ xuất hiện:

$\sqrt{a(b+1)}+\sqrt{b(c+1)} \le \sqrt{(a+1)[(b+1)+b(c+1)]}$

Như thế ta chỉ cần chứng minh:

$\sqrt{b(c+2)+1}+\sqrt{c} \le \frac{3}{2}\sqrt{(b+1)(c+1)}$

$\Leftrightarrow \sqrt{bc+2b+1}+\sqrt{c}\le\sqrt{[bc+2b+1+(c+1)][1+\frac{c}{c+1}]}=\sqrt{\frac{(b+1)(c+2)(2c+1)}{c+1}}$

Như vậy chỉ còn chứng minh:

$\sqrt{\frac{(c+2)(2c+1)}{c+1}}\le\frac{3}{2}\sqrt{c+1}$

Dễ chứng minh bằng tương đương.

Dùng bất biến, đơn biến để giải bài toán tổ hợp - Phần 2

1) Cho tập hợp {3,4,12}. Mỗi bước chọn 2 số a,b rồi thay bởi 0,6a-0,8b và 0,8a+0,6b. Hỏi có thể đạt được:

a) {4,6,12}

b) {x,y,z} với |x-4|, |y-6|, |z-12| đều nhỏ hơn hơn $1/\sqrt{3}$

Giải:

Ta có $(0,6a-0,8b)^2+(0,8a+0,6b)^2=a^2+b^2.$
$3^2+4^2+12^2=13^2$
Suy ra các điểm có dang (a,b,c) nằm trên hình cầu quanh O với bán kính 13

$4^2+6^2+12^2=14^2$ nên không thể đạt được a) Do $4^2+6^2+12^2$ khác đại lượng bất biến đó.

b) Do $(x-4)^2+(y-6)^2+(z-12)^2<1$ nên

Nhận xét: Điều quan trọng bất biến ở đây là khoảng cách từ điểm (a,b,c) đến O.

2) Cho bàn cờ 8x8 được tô trắng đen. Hỏi có thể tô sao cho còn một ô đen không, nếu:

a) Đổi màu lại tất cả ô trong 1 hàng hoặc cột.

b) Đổi màu lại (trắng thành đen, đen thành trắng) tất cả các ô của ô vuông 2x2 bất kì.

Giải:

a) Chọn một hàng và một cột giả sử ô đó có b đen và 8-b trắng thì sau khi đổi sẽ có b trnawgs và 8-b đen. số lượng ô đen thay đổi bằng |(8-b)-b| là một số chẵn. Nên tính chẵn lẻ của số ô đen không đổi. 1 ô đen là số chẵn. Ban đầu có số chẵn ô đen nên không được.

b) Giả sử ô 2x2 có 1 ô đen, 2 ô đen, 3 ô đen, 4 ô đen thì chứng minh rằng sau khi đổi màu số ô đen cũng là số chẵn nên ta có đáp án cũng là không được.

Lưu ý: bàn cờ ta xét được tô trắng đen như bàn cờ vua.

3) Trên vòng tròn có 5 số 1 và 4 số 0 được sắp xếp tùy ý. Sau đó ta thực hiện phép biến đổi sau. Giữa hai số giống nhau điền số 0, giữa hai số khác nhau điền số 1. Cuối cùng xóa 9 số ban đầu đi ta được 9 số mới. Chứng minh sau hữu hạn bước không thể có 9 số 0.

Giải

Ta sẽ đi ngược:

(0,0,..0) <- (1,1,1....1) <-(1,0,1,0,..1,0) phải có tổng số số 0 và 1 là số chẵn mà 4+5=9 nên không tồn tại.

4) Cho bảng hình chữ nhật, mỗi ô ta ghi một số nguyên dương. Với mỗi bước, bạn có thể nhân đôi tất cả các số trên hàng hoặc giảm 1 từng số của cột nào đó. Chứng minh rằng sau hữu hạn bước ta sẽ thu được bảng toàn chữ số 0.

Giải

Xét cột đầu tiên. Nếu số nhỏ nhất côt đó không phải 1 ta giảm cho bằng 1. Nếu có một số số 1 ở cột đó thì ta nhân hai tất cả các số tương ứng ở hàng chứa số 1. Rồi sao đó giảm 1 đơn vị ở cột đầu tiên. Cứ như vậy ta sẽ thu được cột đầu tiên tất cả chữ số 1. Rồi giảm 1 đơn vị ta sẽ có tất cả số 0 cho cột. Tương tự cột tiếp theo

5) Một hàng ta viết 1000 số nguyên. Dưới mỗi số a ở hàng đầu, là một số nguyên f(a) sao cho f(a) là số lần xuất hiện của a ở hàng đầu. Tương tự ta có hàng thứ 3 từ hàng thứ 2,vv, Chứng minh rằng, cuối cùng sẽ có một hàng giống y như hàng trước nó.

Giải:

Như hình vẽ ví dụ, ta thấy rằng dưới chữ số a của hàng 2 thì sẽ có số b ở hàng 3 sao cho $b \ge a$

Ta có dãy trên là dãy tăng như lại bị chặn trên nên sẽ có một hàng y hệt hàng trước.

6) Một bàn cờ vua 8x8. Mỗi bước, có thể chọn 4x4 hoặc 3x3 và cộng thêm 1 vào mỗi số nguyên trong hình vuông đó ( Bàn cờ vua có điền số nguyên). Hỏi có thể luôn luôn nhận được một bàn cờ với:

a) tất cả các số đều chia hết cho 2 ?

b) tất cả các số đều chia hết cho 3 ?

Giải:

 a) Ta đặt S là tổng các số trong ô vuông trừ hàng 3 và hàng 6 thì số dư của S mỗi lần thay đổi là bất biến. Nên nếu tổng lúc đầu lẻ thì ta không thu được (Số dư S cho 2)

b) Tương tự ta đặt S là tổng các số trong ô vuông trừ hàng 4 và 8 thì số dư của S cho 3 mỗi lần thay đổi là bất biến nên nếu tỏng S không chia hết cho 3 ta cũng có đpcm

7) Cho (m,n)=1. Bắt đầu với m số nguyên, chọn n số nguyên trong chúng và cộng một vào mỗi số (n<m). Hỏi sau một số lần lặp lại thì có thể nhận được m số nguyên toàn bằng nhau không ?

Giải:
Có. Theo định lí bezout ta có: nx=my+1. Giờ ta viết $x_1,..x_m$ trên vòng tròn theo chiều kim đồng hồ và $x_1 \le x_2 \le..\le x_m$. Ta bắt đầu từ$x_1$ tới $x_n$ tăng 1 đơn vị như vậy một số lần ta sẽ có tất cả các số đều tăng 1 đơn vị như còn dư một số$x_m$. Như vậy $x_{max}-x_{min}$=1 như vậy sau một số lần nó sẽ giảm đến 0 và ta có đpcm.

8) Các số 1,2..2n được xếp theo thứ tự tùy ý vào các nơi được đánh dấu sẵn: 1,2 ..2n. Giờ ta cộng số ô đánh dấu và số trong ô đánh dấu. Chứng minh rằng bao giờ cũng có hai tổng có cùng số dư khi chia cho 2n.

Giả sử không có, thì các tổng có số dư là 0,1,2,3..2n-1.

Tổng tất cả các tổng đó bằng: 2(1+2+..2n-1)=2n(2n+1) chia hết 2n

Tổng các số dư khi cho cho 2n lại bằng n(2n-1) không chia hết cho 2n

Vô lí, vậy ta có đpcm

Dùng hàng điểm để chứng minh thẳng hàng.

Bài toán: Cho tam giác ABC nhọn tâm đường tròn ngoại tiếp O, trực tâm H, đường cao AD. AO cắt
BC tại E. đường thẳng qua D song song OH lần lượt cắt AB,AC tại M,N. I là trung iểm
AE. DI lần lượt cắt AB,AC tại P,Q. MQ cắt NP tại T. Chứng minh rằng D,O, T thẳng
hàng.

Trần Quang Hùng

Đ ại học Khoa học Tự nhiên, Đ HQGHN

Lời giải:

Gọi F là trung điểm BC.

Theo một số kết quả cơ bản ta có $\overrightarrow{AG}=\overrightarrow{OF}$ Suy ra AE song song GF suy ra DI đi qua trung điểm J của GF, mà ta lại có CHOF là hình bình hình hành nên DI đi qua trung điểm HO.

DO cắt AB, AC tại K, L.

Ta có $D(HOJN) = (HOJ) = −1.$ (DN song song HO)

$(AKMP) = D(AKMP) = D(ALNQ) = (ALNQ) = D(HOJN) = −1$

Khi (AKMP) = −1 ta cũng có (AKPM) = −1. Vậy từ hai đ ẳng thức trên ta có (AKPM) =
(ALNQ) hay KL, PN,MQ đồng quy tại T, nói cách khác D,O, T thẳng hàng. Ta có điều
phải chứng minh.

Dùng đường đối trung để giải bài toán.

Cho tam giác ABC nhọn, BE,CF là các đường cao. M là trung đ iểm của BC. N là giao

của AM và EF. X là hình chiếu của N trên BC. Y,Z theo thứ tự là hình chiếu của X trên

AB,AC. Chứng minh rằng N là trực tâm của tam giác AY Z.

Gọi K là hình chiếu của M lên EF. Thì K là trung điểm EF.

Ta có tam giác AKF đồng dạng tam giác AMC (c.g.c), kết hợp với tức giác KMNX nội tiếp ta có:

$\angle AKX=\angle AKF+\angle EKX=\angle AMB+\angle AMC=180^o$

Nên $A, K, X$ thẳng hàng.

Dùng AX là đối trung kết hợp tứ giác  AXYZ nội tiếp xuy ra AN vuông YZ

Ngoài ra $NE/NF=AE^2/AF^2=AB^2/AC^2=XB/XC=YB/YF$

Nên ta có NY song song BF hay NT vuông AZ.

Vậy ta có đpcm

Nhận xét: Qua bài này ta cần lưu ý kết quả sau, đường đối trung của tam giác ABC đi qua trung điểm EF.

Dùng đơn biến và số dư để giải bài toán tổ hợp

Bài toán: Bắt đầu với dãy: S=(a,b,c,d) của các số nguyên không âm. Đặt $S_1=T(S)=(|a-b|,|b-c|,|c-d|,|d-a|)$. Tương tự $S_2=T(S_1)$. Hỏi có tồn tại $S_i$ sao cho $S_i=(0;0;0;0)$

Giải

Chúng ta thử vài trường hợp:

(0, 3, 10, 13) → (3, 7, 3, 13) → (4, 4, 10, 10) → (0, 6, 0, 6) → (6, 6, 6, 6) → (0, 0, 0, 0)

 (8, 17, 3, 107) → (9, 14, 104, 99) → (5, 90, 5, 90) → (85, 85, 85, 85) → (0, 0, 0, 0),

(91, 108, 95, 294) → (17, 13, 99, 203) → (4, 86, 104, 186) → (82, 18, 82, 182) → (64, 64, 100, 100) → (0, 36, 0, 36) → (36, 36, 36, 36) → (0, 0, 0, 0).

1) Đặt max S là phần tử lớn nhất của S. Khi đó $max S_{i+1} \le max S_i$ và $max S_{i+4}< max S_i$ ( Vì khi  $max S_{i+1} = max S_i$ Khi  $(S_i=(0, S_{i+1},a,b)$ tới $S_{i+3}$ nó sẽ giảm)

2)  Sau nhiều nhất 4 bước, tất cả 4 số sẽ trở thành số chẵn. Thật vậy ta sẽ xét đồng dư 2. Do tính đối xứng nên ta chỉ xét trường hợp này ( các trường hợp khác tương tự) :
0001 → 0011 → 0101 → 1111 → 0000 và 1110 → 0011. Vì thế sau nhiều nhất 4 bước tất cả các số sẽ chia hết cho 2, sau nhiều nhất 8 bước chia hết $2^2$,..sau nhiều nhất 4k bước thì các số sẽ chia hết $2^k$ cho k thật lỡn ta sẽ có tất cả cá số đều bằng 0

Dùng bất biến, đơn biến để giải bài toán tổ hợp - Phần 1

1) Cho n là số tự nhiên lẻ. Đầu tiên bạn A viết các số 1,2,..2n lên bảng. Sau đó bạn ấy chọn hai số a, b bất kì, xoá nó và viết lại số |a-b|, Chứng minh rằng chữ số cuối cùng còn lại là một số lẻ.

Lời giải:

Đặt $S=1+2+..2n=n(2n+1)$ lẻ. Mỗi bước thực hiện ta có $S'=S+|a-b|-a-b=S-2min(a,b)$. Vì vậy tính chẵn lẻ của S là bất biến. Số cuối cùng phải đồng dư 1 mod 2.

2) Một vòng tròn được chia thành sáu phần. Sau đó, các con số 1, 0, 1, 0, 0, 0 được viết
vào các phần (ngược chiều kim đồng hồ). Bạn có thể làm tăng hai số kề nhau một số bằng 1.Có thể cân bằng các số sau hữu hạn bước hay không ?

Lời giải:

Giả sử $a_1, a_2,..a_6$ là các số trên các phần đó. Ta có: $I=a_1 −a_2 +a_3 −a_4 +a_5 −a_6$ là một đại lượng bất biến. Ban đầu $I=2$ nên không thể cho $I=0$ được

3) Trong Quốc hội Sikinia, mỗi thành viên có ít nhất ba kẻ thù. Chứng minh
rằng ngôi nhà có thể được chia thành hai ngôi nhà, để mỗi thành viên có ít nhất
một kẻ thù trong chính ngôi nhà của mình.

Lời giải:

Ban đầu cho bất kì các thành viên vào hai ngôi nhà.

Đặt H là tổng số của tất cả các kẻ thù của mỗi thành viên đều có trong chính ngôi nhà của mình.

Bây giờ giả sử A có ít nhất hai ( có thể 3)  kẻ thù trong nhà của mình. Khi đó, A sẽ có ít nhất 1 kẻ thù trong nhà khác. Nếu A chuyển nhà, số H sẽ giảm (Tăng 1 giảm 2). Điều này giảm không thể mãi mãi. Tại một số thời gian, H đạt tối thiểu tuyệt đối của nó.
Sau đó, chúng ta đã đạt đến phân phối yêu cầu.

4) Giả sử các số a,b,c,d không đồng thời bằng nhau.Bắt đầu với (a, b, c, d) và
nhiều lần thay thế (a, b, c, d) bằng cách (a - b, b - c, c - d, d - a). Sau đó ít nhất một trong 4
số sẽ lớn vô cùng

Lời giải:
Đặt $P_n=(a_n, b_n, c_n, d_n)$ là 4 số sau khi đổi n lần. Khi đó ta có: $a_n+b_n+c_n+d_n=0$ (với $n \ge 1$)
Chúng ta không nhìn thấy cách nào để sử dụng bất biến... Nhưng nếu nhìn theo hướng hình học thì thật hữu ích. Chức năng rất quan trọng cho các điểm $P_n$ trong không gian 4 chiều là khoảng cách tử điểm đó đến điểm gốc là $(0;0;0;0)$ là: $a_n^2+b_n^2+c_n^2+d_n^2$. Nếu ta chứng minh nó không có giới hạn trên ta có điều phải chứng minh.

Ta sẽ cố gắng tìm mối liên hệ giữa $P_n$ và $P_{n+1}$:

$\sum a_{n+1}^2=\sum (a_n-b_n)^2=2\sum a_n^2-2\sum a_nbn$

Mặt khác:

$0=(\sum a_n)^2=(a_n+c_n)^2+(b_n+c_n)^2+2\sum a_nb_n$

Cộng hai vế lại suy ra: $ \sum a_{n+1}^2\ge\sum a_n^2$

Như vậy ta kết luận rằng với $n \ge 2$

$\sum a_n^2\ge2^{n-1}\sum a_1^2$

Như vậy khoảng cách từ điểm $P_n$ đến điểm gốc tăng không có giới hạn trên. Tức là phải có một số đạt đến vô cùng.

5) Có 2n  đại sứ được mời đến một bữa tiệc. Mỗi đại sứ có nhiều nhất n-1
kẻ thù. Chứng minh rằng các đại sứ có thể được ngồi quanh một chiếc bàn tròn, để
không ai ngồi cạnh một kẻ thù.

Giải

Đầu tiên chúng ta xếp chỗ ngồi các đại sứ bất kì. Gọi H là số cặp đôi thù địch ở gần nhau. Chúng ta phải tìm ra một thuật toán làm giảm số này bất cứ khi nào H> 0. Đặt (A, B) là một cặp thù địch với B ngồi bên trái của A (Như trong hình Fig 1.3). Chúng ta phải tách chúng ra để gây ra ít xáo trộn càng tốt. Điều này sẽ đạt được nếu chúng ta đảo ngược cung BA' nhận được hình Fig 1.4, H sẽ được giảm nếu (A,A') và (B, B') trên hình Fig 1.4 là cặp đôi thân thiện. Mà với A ta lại có ít nhất n bạn. Mà họ không thể là kẻ thù của B được nên có bạn A' của A lại là bạn của B, bên phải B'- bạn của B.

Dùng tính liên tục của tổ hợp để giải bài toán.

Ví dụ: Cho bảng vuông nxn gồm$n^2$ ô vuông đơn vị. Điền vào các ô đơn vị các số nguyên sao cho hai ô cạnh nhau (có cạnh chung) được điền vào hai số chênh lệch nhau không quá 
$1$ đơn vị. Chứng minh rằng có một số xuất hiện ít nhất $n$ lần.

Ta sẽ giải bằng nguyên lí cực hạn kết hợp với tính liên tục của nó:

Trên mỗi hàng chọn ra số lớn nhất. Gọi số bé nhất trong các số đó là $a$

Trên mỗi hàng chọn ra số bé nhất. Gọi số lớn nhất trong các số đó là $b$

Trên mỗi cột chọn ra số lớn nhất. Gọi số bé nhất trong các số đó là $c$

Trên mỗi cột chọn ra số bé nhất. Gọi số lớn nhất trong các số đó là $d$

Trước hết ta chứng minh $c\ge b$

Thật vậy gọi $e$ là số nằm trên cột chứa $c$ và hàng chứa $b$

Khi đó theo cách gọi $c\ge e,e\ge b$ suy ra $c\ge b$

Tương tự $a\ge d$ 

TH1 : $a>b$

Gọi $x$ là một số bất kỳ nằm giữa $a$ và $b$

Khi đó dễ thấy hàng nào cũng phải chứa $x$ (Vì trên mỗi hàng $x$ đều không nhỏ hơn số bé nhất của hàng đó và không lớn hơn số lớn nhất của hàng đó) 

Khi đó $x$ lặp lại $n$ lần

TH2 :$a\le b$

-Nếu $c>d$ thì xét tương tự TH1

-Nếu $c\le d$ 

Theo trên ta có: $c\ge b\ge a\ge d$

Từ đây dễ suy ra $a=b=c=d$ suy ra cả $n^2$ số trên bảng đều bằng nhau

 Vậy tồn tại một số xuất hiện ít nhất $n$ lần 

Nhận xét : cách giải ở trường hợp ta $a>b$ đã dùng tính liên đó là từ a đến b chắc chắn phải đi qua x. Xét trên một hàng bất kì. Thì  số nhỏ nhất $\ge b \ge x  \ge a \ge$ số lớn nhất nên từ số nhỏ nhất đến số lớn nhất thì luôn tăng hoặc giảm 1 đơn vị nên chắc chắn phải đi qua x.

link nguồn: http://diendantoanhoc.net/topic/158120-ch%E1%BB%A9ng-minh-r%E1%BA%B1ng-c%C3%B3-m%E1%BB%99t-s%E1%BB%91-xu%E1%BA%A5t-hi%E1%BB%87n-%C3%ADt-nh%E1%BA%A5t-n-l%E1%BA%A7n/#entry632412