Bài toán về sự phân bố số chính phương và số nguyên tố

Bài toán: Xét tất cả các số nguyên tố $p_1 < p_2 <..p_n<..$ Đặt $a_n=p_1+p_2+..+p_n$. Chứng minh rằng với mọi n nguyên dương, nằm giữa $a_n$ và $a_{n+1}$ có ít nhất một số chính phương.

Giải:
Bổ đề: Với $n \ge 4$ thì $p_{n+1} > 2\sqrt{p_1+p_2+..+p_n}+1$
Chứng minh:
Với n=4, đúng.

Giả sử đúng với n=k tức là:
$p_{k+1} > 2\sqrt{p_1+p_2+..+p_k}+1$

Hay là $(p_{k+1}-1)^2 >4 (p_1+p_2+..+p_k)$

Ta cần chứng minh: $(p_{k+2}-1)^2 >4 (p_1+p_2+..+p_{k+1})$

Hay chỉ cần chứng minh: $(p_{k+2}-1)^2 \ge (p_{k+1}-1)^2 +4p_{k+1}$

Điều này tương đương $(p_{k+2}-p_{k+1})(p_{k+2}+p_{k+1}-2) \ge 4p_{k+1}$

Điều này là hiển do khoảng cách 2 số nguyên tố liên tiếp bé nhất là 2. Vậy ta có đpcm

Quay lại bài toán
Với n=1, thì giữa 2 và 5 tồn tại 4 là số chính phương.
Tương tự cho n=2,3,4

Giả sử đúng với n=k tức là giữa $a_k$ và $a_{k-1}$ tồn tại ít nhất một số chính phương, ta gọi $a^2$ là số chính phương lớn nhất trong các số chính phương đó.

$(a+1)^2 > a_{k}$

Áp dụng bổ đề thì $p_{k+1}>2a+1$ nên $a_{k+1} >(a+1)^2$.

Bài toán đường thẳng qua tâm và đề thi PTNK

(PTNK 2014 -2015) Cho $\triangle ABC$ không cân.Gọi $I$ là trung điểm $BC$.Đường tròn $(I,IA)$ cắt $AB,AC$ lần lượt tại $M,N$.$MI,NI$ lần lượt cắt $(I)$ tại $P,Q$.Gọi $K$ là giao của $PQ$ với tiếp tuyến tại $A$ của $(I)$.Chứng minh $K$ nằm trên $BC$.

Lời giải:

Ta dễ thấy ngay $KA$ là trục đẳng phương của $(I)$ và đường tròn đường kính $AI$.Từ đó ý tưởng phương tích-trục đẳng phương là sáng sủa nhất.

[IMG]

[/IMG]

Kẻ đường kính $AA'$ của $(I)$.Khi đó các tứ giác:$AMA'P$,$ANA'Q$ và $ABA'C$ là hình bình hành nên $A',C,P$ và $A',B,Q$ thẳng hàng.

Từ đó $\angle AQB=\angle APC=90$.

Kẻ đường cao $AH$ thì $H \in (ABQ),(ACP)$

Từ đó: $\angle QHB=\angle QAB=\angle QPM$

Suy ra $QHIP$ là tứ giác nội tiếp.

Do đó $HI$ là trục đẳng phương của đường tròn đường kính $AM$ và $(QHIP)$.

Và thêm nữa là $PQ$ là trục đẳng phương của $(I)$ và $(QHIP)$.

Từ đó thì $AK,PQ,HI$ đồng qui nên ta có đpcm.

Để ý thì ta sẽ thấy tam giác AMN có BC là đường thẳng qua tâm, có thể dùng Pascal để chứng minh QB, CP cắt nhau tại A' thuộc (I) nhưng chưa chỉ ra được AA' là đường kính có thể chỉ ra bằng cách do QB // CN. Như vậy bài toán là cách dựng tam giác ABC nội tiếp (O) và đường thẳng sao cho d đi 

qua tâm và cắt AB, AC tại E, F sao cho O là trung điểm EF.

Dùng dãy số để giải phương trình hàm

(PTNK 2014) Tìm tất cả các hàm số f: N* --> N* thỏa mãn hệ thức $ f(f(n)/n) = n^2 $ với mọi n nguyên dương. N* ký hiệu tập hợp các số nguyên dương.

Giải:

Đặt $f(n)=ng(n)$ thì $g: N^*-> N^*$.
Khi đó $f(\frac{f(n)}{n})=n^2 \Leftrightarrow  g(n)g(g(n))=n^2$.
Lấy logarit hai vế ta có: $ ln{g(n)}+ln{g(g(n))}=2ln{n}$.
Đến đây ta xét dãy sau:
$u_0=ln{x};x\in N^*$ và $u_n=ln{g_n(x)}$ trong đó $g_n(x)=g(...g(n)...)$ với n lần lấy hàm g.
Ta có: $u_n\geqslant0$ và $u_{n+2}+u_{n+1}-2u_n=0$.
Công thức tổng quát: $u_n=\frac{2ln{x}+ln{g(x)}}{3}+\frac{ln{x}-ln{g(x)}}{3}(-2)^n$.
Nếu tồn tại $x$ sao cho $ln{x}-ln{g(x)}<0$ thì $u_{2n}<0$ với n đủ lớn (mt)
Nếu tồn tại $x$ sao cho $ln{x}-ln{g(x)}>0$ thì $u_{2n+1}<0$ với n đủ lớn (mt).
Vậy $ln{g(x)}=ln{x}$ với mọi $x \in N^*$. Suy ra $f(n)=n^2$

Dùng tam thức bậc 2 để chứng minh bất đẳng thức

(Quảng Trị 2014) Chứng minh bất đẳng thức sau $3(x^2-x+1)(y^2-y+1) \ge 2(x^2y^2-xy+1)$ với mọi x, y thực.

Lời giải:

Có

$P = 3  (x^2-x+1 ) ( y^2-y+1) - 2( x^2y^2 - xy+1)=( y^2-3y+3 ) x^2 + ( 5y-3y^2-3 ) x + 3y^2-3y+1$

Có $ \displaystyle y^2 -3y+3 > 0 $ và

$$ \Delta = -3 \left( y^2- 3y+1 \right)^2 \le 0 $$

Nên

$$ P \ge 0 $$

Đó là điều cần chứng minh .

Định lý Hensen

Định lý Hansen được phát biểu như sau (tham khảo trong Một số kiến thức về hình học phẳng trong các cuộc thi OLYMPIC Toán):

Cho tam giác ABC có r là bán kính đường tròn nội tiếp, $r_a, r_b, r_c$ là các bán kính đường tròn bàng tiếp. Khi đó các khẳng định sau là tương đương:

1. Tam giác ABC vuông.
2. $r+r_a+r_b+r_c=a+b+c$
3. $r^2+r_a^2+r_b^2+r_c^2=a^2+b^2+c^2$

Giải:

Trước hết gọi $(I), (I_a), (I_b), (I_c)$ lần lượt là tâm đường tròn nội tiếp, bàng tiếp góc A, bàng tiếp góc B, bàng tiếp góc C của tam giác ABC.

Gọi D là trung điểm BC, N là trung điểm $I_bIc$ Khi đó áp dụng tính chất đường trung bình của hình thang $2ND=r_b+r_c$

Mà $ND=R+OD=R+\frac{AH}{2}$ (H là trực tâm của tam giác ABC)

Mặt khác: Gọi X là tiếp điểm của (I) với BC, X' là tiếp điểm của $(I_a)$ với BC.

I' đối xứng I qua O.

M là giao điểm của $II_a$ và (O).

Ta có $2OD=I'X'+IX=r+2R-r_a$ Do $I'X'=2R-r_a$

Kết hợp tất cả những gì chứng minh ta có các đẳng thức sau:

a) $r_a+r_b+r_c=4R+r$

b) $AH = 2R + r − r_a, BH = 2R + r − r_b, CH = 2R + r − r_c.$

Như vậy 1. Tương đương $AH+BH+CH+2R=a+b+c$

$2R(cosA+cosB+cosC)=2R(sinA+sinB+sinC)$

Tương đương $(sin\frac{C}{2}-cos\frac{C}{2})(cos\frac{A-B}{2}-cos\frac{C}{2}))=0$

Điều phải chứng minh.

2. Tương đương $ (2R + r − r_a)^2+(2R + r − r_b)^2+(2R + r − r_c)^2+4R^2=a^2+b^2+c^2$

$ (2R + r − r_a)^2+(2R + r − r_b)^2+(2R + r − r_c)^2+4R^2-(a^2+b^2+c^2))$
$= 4R^2(cos^2 A + cos^2 B + cos^2 C + 1 − sin^2 A − sin^2 B − sin^2 C)$
$= − 16R^2 cos A cos B cos C=0.$

Như vậy tam giác ABC vuông.

Vậy ta có đpcm.

Tìm giới hạn dãy số

Bài 1 (Đề thi chọn đội tuyển Amsterdam 2016) Cho dãy số thực $(x_n)$:

$\left\{\begin{matrix}
x_1=3 &  & \\
x_{n+1}=\frac{3x_n-1}{x_n} &  &
\end{matrix}\right.$ Xét dãy số:

$y_n=\frac{(3+\sqrt{5})^n}{2^n.x_1x_2..x_n}$ Chứng minh rằng dãy $(y_n)$ có giới hạn hữu hạn và tìm giới hạn đó.

Bài giải:




Xét $f(x) = \frac{3x-1}{x} $

Có $f'(x) = \frac{1}{x^2 } >0 $

Mà mặt khác ta có $x_2 < x_1 => x_n giảm $

Mặt khác, ta có $x_1 \geq \frac{3+\sqrt{5}}{2} $

Giả sử $x_n \geq \frac{3+\sqrt{5}}{2} $ đúng với $n$, ta chứng minh đúng với $n+1 $

Tức là chứng minh

$\frac{3x_n-1}{x_n} \geq \frac{3+\sqrt{5}}{2} <=> x_n \geq \frac{3+\sqrt{5}}{2} $

Do đó ta có $x_n$ giảm, bị chặn dưới bởi $\frac{3+\sqrt{5}}{2} $ do đó, tồn tại $L$ bằng $lim x_n $

Mà khi chuyển sang giới hạn, ta tính đc $L=\frac{3+\sqrt{5}}{2} $

Mặt khác $\frac{y_{n+1}}{y_n } = \frac{3+\sqrt{5}}{2x_{n+1}} \leq 1$

Do đó $y_n $ giảm, bị chặn dưới bởi $0$

Suy ra tồn tại $L'= lim y_n $

Thay vô $L'=\frac{3+\sqrt{5}}{2L} . L' => L'=0 $

Các bài bất đẳng thức trong đề thi hsg tỉnh, thành phố

Bài 1 (Thái Bình) : Cho a,b, c là các số thực dương thỏa mãn abc=1. Chứng minh rằng:

$\sum \frac{(3a-1)^2}{2a^2+1}\ge4$

Bài 2: (TP HCM) Chứng minh rằng với mọi a,b, c dương ta đều có:

$\sum \frac{1}{a(1+b)}\ge\frac{3}{1+abc}$
Bài 3: (PTNK): Cho a,b,c dương thỏa mãn: ab+bc+ca=1. Chứng minh rằng:

$\sum \frac{1}{3+2(a^2-bc)}\ge1$
Giải:

Bài 1: Áp dụng bất đẳng thức C-S ta đưa về chứng minh:

$(a^2+b^2+c^2)+18(ab+bc+ca-a-b-c)-3 \ge 0$

Đặt VT= f(a,b,c), đặt $t=\sqrt{ab}$

$f(a,b,c)-f(t,t,c)=a^2+b^2-2ab+18((c-1)(a+b)-(c-1)2t) \ge 0 $ Đúng nếu ta giả sử c=max

Như vậy ta chỉ cần chứng minh:

$2t^2+c^2+18(t^2+2tc-2t-c)-3 \ge0 $

Do $c.t^2=1$

Sau khi rút gọn ta sẽ đưa về:
$(t-1)^2(t+1)(5t+1)(2t-1)^2 \ge 0$

Dấu bằng xảy ra khi và chỉ khi a=b=c=1, a=b=1/2, c=4

Bài 2:

Bất đẳng thức tương đương:

$\sum \frac{1+abc}{a(1+b)}\ge 3 \Leftrightarrow \sum (1+\frac{1+abc}{a(1+b)})\ge 6\\\Leftrightarrow \sum (\frac{a+1+ab(c+1)}{a(1+b)})\ge 6 \Leftrightarrow \sum (\frac{a+1}{a(1+b)}+\frac{a(b+1)}{1+a})\ge6$ (đúng theo AM-GM)

Bài 3:

Đặt ab=x, bc=y, ca=z ta đưa về bất đẳng thức:

x,y,z dương thỏa mãn x+y+z=1, và:

$\sum \frac{x}{3x+2yz-x^2}\ge1$

Nhận xét mẫu số là số dương do 3x+2yz-x^2=3x(x+y+z)+2yz-x^2 >0. Áp dụng bdt C-S:

$\sum \frac{x}{3x+2yz-x^2}\ge \frac{(x+y+z)^2}{3(x^2+y^2+z^2)-2(x^3+y^3+z^3-3xyz)}=\frac{1}{3(x^2+y^2+z^2)-2(x^2+y^2+z^2-xy-yz-zx)}=1$

Định lý Dirichle

(Định lí Dirichle) Cho $\alpha$ là một số vô tỉ. Chứng minh rằng, tồn tại vô hạn các số nguyên p,q với q>0 sao cho:

$|\alpha -\frac{p}{q}| <\frac{1}{q^2}$

Lời giải:

Trước hết ta chứng minh với mọi $ N \ge q$ luôn tồn tại p,q thỏa mãn:

$|\alpha -\frac{p}{q}| <\frac{1}{qN}$

Thật vậy ta chia các [0;1) thành các khoảng $[\frac{k-1}{N};\frac{k}{N})(k =\overline{1,N})$

Thì theo nguyên lý Dirichle sẽ tồn tại hai số { $\alpha q_i$ } và { $\alpha q_j$ } thuộc vào một đoạn (  q= 0,1,..N)

$\Rightarrow \left | \begin{Bmatrix}
\alpha q_i
\end{Bmatrix}- \begin{Bmatrix}
\alpha q_j
\end{Bmatrix} \right |<\frac{1}{N(q_i-q_j)}\\\Rightarrow \left | \alpha -\frac{\begin{bmatrix}
\alpha q_i
\end{bmatrix}-\begin{bmatrix}
\alpha q_j
\end{bmatrix}}{q_i-q_j} \right | <\frac{1}{N(q_i-q_j)}$ Điều phải chứng minh.

Ta giả sử chỉ có hữu hạn các số p,q thỏa mãn đề bài Kí hiệu tập này là X.

Khi đó sẽ tồn tại M sao cho $|\alpha -\frac{p}{q}| >M$

Chọn N sao cho $\frac{1}{M}<N$ Khi đó tồn tại các số nguyên dương $p_i, q_i$ sao cho
$|\alpha -\frac{p_i}{q_i}| <\frac{1}{q_iN} <\frac{1}{q_iN}<\frac{1}{q_i^2}$

Suy ra $p_i,q_i$ thuộc X, nhưng $M >\frac{1}{q_iN} $ (mâu thuẫn)

Vậy ta có điều phải chứng minh.

Định lý Brocard để chứng minh bài toán liên quan đến trực tâm

Bài toán: Cho tam giác 
$ABC$ nhọn với đường cao $AD,BE,CF$ đồng quy tại $H$. $DE,DF$ lần lượt cắt $AB,AC$ tại $P,Q$. $R$ là trung điểm $PQ$. $N$ là tâm đường tròn ngoại tiếp tam giác $DEF$. Gọi $HN$ cắt $AR$ tại $L$. Chứng minh rằng trực tâm tam giác $ALN$ nằm trên $EF$.

Lời giải:

Gọi $X,Y$ lần lượt là trung điểm của $AC,AB.K$ là giao điểm của $XY$ với $EF$. Ta sẽ chứng minh $K$ là trực tâm của tam giác $ALN$.

Ta có $QF.QD=QA.QC$ nên $Q$ thuộc trục đẳng phương của $(ABC)$ và $(N)$. Tương tự ta suy ra $PQ$ là trục đẳng phương của $(ABC)$ và $(N)$.

Do đó $PQ$ vuông góc với đường thẳng $Euler$ của tam giác $ABC$.




Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$. Do $KX.KY=KE.KF$ nên $K$ thuộc trục đẳng phương của $(AO)$ và $(AH)$.

Từ đó $AK$ vuông góc với đường thẳng $Euler$ của tam giác $ABC$ hay $AK\parallel PQ$. Mặt khác do $AK\perp OH$ nên $AK\perp NH$

Theo định lí $Brocard$ ta suy ra $EY,FX$ cắt nhau trên $OH$. Lại có $A(QPRK)=-1$ nên $A(QLRK)=-1$ từ đó $L$ là giao điểm của $EY,FX$.

Theo định lí $Brocard$ ta có điều phải chứng minh. $\blacksquare$

Một số chú ý về tứ giác toàn phần và bài toán thi Olympic nữ sinh châu Âu

Chúng ta thường làm việc với tứ giác ABCD với E là giao của hai cạnh bên AB và CD, F là giao của hai cạnh bên AD, BC. Thì chúng ta sẽ có các đường thẳng guass trung điểm hai đường chéo AC, BD và trung điểm EF thẳng hàng, đường thẳng steiner là đường thẳng chứa trực tâm của tam giác FAB, FCD, EAD, EBC thẳng hàng và vuông với đường thẳng guass của tứ giác, ngoài ra ta còn các định lý Miquel, đường tròn Miquel cho tứ giác ABCD.

Và một điều thú vị là nếu ta thay hai cạnh bên AD, BC là hai đường chéo thì ta lại có những tính chất như tứ giác ABCD có AC, BD là hai đường chéo.

Những tính chất nhìn rất mới lạ do hai đường chéo lại là hai cạnh bên của tứ giác ! Vì thế trong một số đề thi chẳng hạn China TST 1992 dùng tính chất đường tròn (ECB) cắt đường tròn (EAD) làm đề thi. Và ta sẽ xét đề thi Olympic toán dành cho nữ sinh ở châu Âu năm 2014

Đề: Cho D, E là các điểm trên AB, AC của tam giác ABC sao cho DB=BC=CE. CD và BE cắt nhau tại F. Chứng minh rằng tâm nội tiếp của tam giác ABC, DEF và trung điểm M của cung lớn BC của đường tròn ngoại tiếp tam giác ABC thẳng hàng.

Lời giải:

Để ý rằng I cũng trực tâm tam giác FBC.

Xét tứ giác DFBC có DC, BE là hai cạnh bên cắt nhau tại F nên đường thẳng steiner của tứ giác là HI (H là trực tâm tam giác DEF), sẽ là trục đẳng phương của hai đường tròn đường kính là hai đường chéo BD, CE. Mặt khác nếu M là trung điểm cung BC thì M cũng sẽ cùng phương tích với hai đường tròn đường kính BD và CE.

Vậy ta có đpcm.

Ta có thể mở rộng bài toán như sau: Cho tam giác ABC cố định. E, F lần lượt di chuyển trên AC, AB sao cho CE=BF. BE cắt CF tại D. H, K là trực tâm tam giác DEF, DBC. Khi đó HK luôn đi qua một điểm cố định khi E, F di chuyển .

Bài này được tổng quá và phát biểu dưới dạng là tìm yếu tố cố định có phần thú vị hơn. Rõ ràng ta phải đoán nhận điểm cố định vì đường tròn ngoại tiếp tam giác ABC không xuất hiện trong đề bài.

Bài tổ hợp nhỏ

Bài toán: Có một số học sinh xếp thành một vòng tròn. Cô giáo yêu cầu các bạn học sinh đứng cạnh nhau bắt tay nhau. Gọi b là số học sinh nam, g là số học sinh nữ, B là số cặp học sinh nam bắt tay nhau và G là số cặp học sinh nữ bắt tay nhau. Chứng minh rằng: b-g=B-G. 

Lời giải của bài toán rất đơn giản như sau:

Dĩ nhiên số học sinh là $1$ thì không có gì để nói. Ta sẽ xét số học sinh từ $2$ trở lên
i) Với số học sinh là hai, ta xét là TRAI - TRAI, GÁI - GÁI, GÁI - TRAI thì thấy khẳng định bài toán đúng.
ii) Bây giờ giả sử bài toán đúng với số học sinh $n$. Bây giờ ta thêm một em học sinh vô. Vai trò mấy em này như nhau, nên giả sử ta thêm bạn nữ vào
Khi đó $B' = B$ và $G' = G + 1$.
a) TH1. Ta nhét em ấy vào giữa GÁI - GÁI thì $b' = b$ và $g' = g + 1$. Khi đó $B' - G' = B - G - 1 = b - g - 1 = b' - g'$.
b) TH2. Ta nhét em ấy vào giữa TRAI - GÁI thì $b' = b$ và $g' = g + 1$. Tương tự trên ta cũng có đpcm.
c) TH3. Ta nhét em ấy vào giữa TRAI - TRAI thì $b' = b - 1$ và $g' = g$. Lúc đó $B' - G' = B - G - 1 = b - 1 - g = b' - g'$. Xong.

Dùng hàm sinh trong bài toán đếm

Bài 1: $x+2y+3z=n (n \in N) $ có bao nhiêu nghiệm nguyên không âm ?

Giải:

Bổ đề : $\text{Với }|a|<1\text{ thì }\sum_{i=0}^{\infty}a^i=\lim_{n\to\infty}\sum_{i=0}^{n}a^i=\lim_{n\to\infty}(1+a+a^2+...+a^n)=\lim_{n\to\infty}\frac{1-a^{n+1}}{1-a}=\frac{1}{1-a}$

Dùng PP hàm sinh :

Xét $|a|<1$ và $f(a)=\left(\sum_{x=0}^{\infty}a^x\right)\left(\sum_{y=0}^{\infty}a^{2y}\right)\left(\sum_{z=0}^{\infty}a^{3z}\right)$$=\sum_{x=0,y=0,z=0}^{\infty}A_{x,y,z}.a^{x+2y+3z}=\sum_{n=0}^{\infty}A_n.a^n$ (1)Ta thấy số nghiệm của pt(*) tương ứng chính là hệ số $A_n$ của $a^n$ trong khai triển $f(a)$

Mặt khác :

$f(a)=\frac{1}{1-a}.\frac{1}{1-a^2}.\frac{1}{1-a^3}=\frac{1}{(1-a)^3(1+a)(1+a+a^2)}$$=\frac{\frac{1}{8}}{1+a}+\frac{\frac{17}{72}}{1-a}+\frac{\frac{1}{4}}{(1-a)^2}+\frac{\frac{1}{6}}{(1-a)^3}+\frac{\frac{1}{9}(2+a)}{1+a+a^2}$

Mà ta có các khai triển sau (Maclaurin):

$\frac{1}{(1-a)^m}=(1-a)^{-m}=\sum_{k=0}^{\infty}\binom{-m}{k}(-1)^ka^k=\sum_{k=0}^{\infty}C_{k+m-1}^{m-1}a^k$

$\frac{1}{1+a+a^2}=(1-a).\frac{1}{1-a^3}=(1-a).\sum_{k=0}^{\infty}a^{3k}=\sum_{k=0}^{\infty}(a^{3k}-a^{3k+1})$

$\frac{2+a}{1+a+a^2}=(2+a)\sum_{k=0}^{\infty}(a^{3k}-a^{3k+1})=\sum_{n=0}^{\infty}(2a^{3k}-a^{3k+1}-a^{3k+2})$

Suy ra

$f(a)=\frac{1}{8}\sum_{n=0}^{\infty}(-1)^na^n+\frac{17}{72}\sum_{n=0}^{\infty}a^n+\frac{1}{4}\sum_{n=0}^{\infty}(n+1)a^n+\frac{1}{6}\sum_{n=0}^{\infty}\frac{(n+1)(n+2)}{2}a^n$$+\frac{1}{9}\sum_{k=0}^{\infty}(2a^{3k}-a^{3k+1}-a^{3k+2})$ (2)



Đồng nhất các hệ số của $a^n$ trong (1) và (2), ta có :

$\boxed{}$ Nếu $n=3k$ thì $A_n=\frac{(-1)^{3k}}{8}+\frac{17}{72}+\frac{3k+1}{4}+\frac{(3k+1)(3k+2)}{12}+\frac{2}{9}=\frac{3(-1)^k+21+36k+18k^2}{24}$

$\boxed{}$ Nếu $n=3k+1$ thì $A_n=\frac{(-1)^{3k+1}}{8}+\frac{17}{72}+\frac{3k+2}{4}+\frac{(3k+2)(3k+3)}{12}-\frac{1}{9}=\frac{3(-1)^{k+1}+27+48k+18k^2}{24}$

$\boxed{}$ Nếu $n=3k+2$ thì $A_n=\frac{(-1)^{3k+2}}{8}+\frac{17}{72}+\frac{3k+3}{4}+\frac{(3k+3)(3k+4)}{12}-\frac{1}{9}=\frac{3(-1)^{k}+45+60k+18k^2}{24}$




Vậy :

$\boxed{}$ Nếu $n=3k,k=2t$ tức $n=6t$ thì $A_n=\frac{24+72t+72t^2}{24}=1+3t+3t^2=\frac{(n+3)^2+3}{12}=\left\lfloor\frac{(n+3)^2+3}{12}\right\rfloor$

$\boxed{}$ Nếu $n=3k,k=2t+1$ tức $n=6t+3$ thì $A_n=\frac{72+144t+72t^2}{24}=3+6t+3t^2=\frac{(n+3)^2}{12}=\left\lfloor\frac{(n+3)^2+3}{12}\right\rfloor$

$\boxed{}$ Nếu $n=3k+1,k=2t$ tức $n=6t+1$ thì $A_n=\frac{24+96t+72t^2}{24}=1+4t+3t^2=\frac{(n+3)^2-4}{12}=\left\lfloor\frac{(n+3)^2+3}{12}\right\rfloor$

$\boxed{}$ Nếu $n=3k+1,k=2t+1$ tức $n=6t+4$ thì $A_n=\frac{96+168t+72t^2}{24}=4+7t+3t^2=\frac{(n+3)^2-1}{12}=\left\lfloor\frac{(n+3)^2+3}{12}\right\rfloor$

$\boxed{}$ Nếu $n=3k+2,k=2t$ tức $n=6t+2$ thì $A_n=\frac{48+120t+72t^2}{24}=2+5t+3t^2=\frac{(n+3)^2-1}{12}=\left\lfloor\frac{(n+3)^2+3}{12}\right\rfloor$

$\boxed{}$ Nếu $n=3k+2,k=2t+1$ tức $n=6t+5$ thì $A_n=\frac{120+192t+72t^2}{24}=5+8t+3t^2=\frac{(n+3)^2-4}{12}=\left\lfloor\frac{(n+3)^2+3}{12}\right\rfloor$




Tóm lại Số nghiệm tự nhiện của pt $x+2y+3z=n$ là $A_n=\left\lfloor\frac{(n+3)^2+3}{12}\right\rfloor$

Bài 2: Đếm xem có bao nhiêu cách chia 
$32$ cái kẹo giống nhau thành $4$ phần có số lượng khác nhau. (Mỗi phần ít nhất 1 cái kẹo)

Giải:

Gọi $x_1,x_2,x_3,x_4$ lần lượt là số kẹo ở mỗi phần

Không mất tính tổng quát, giả sử $x_1<x_2<x_3<x_4$

Đặt $x_i=x_{i-1}-s_i$, với $i=2,3,4$. Ta có:

$32=x_1+x_2+x_3+x_4=x_1+x_2+2x_3+s_4=x_1+3x_2+2s_3+s_4=4x_1+3s_2+2s_3+s_4$

Ta đưa bài toán từ tìm số bộ nguyên dương $\left ( x_1,x_2,x_3,x_4 \right )$ thành đếm số bộ nguyên dương $\left ( x_1,s_2,s_3,s_4 \right )$

Đặt $y_1=x_1-1$, $y_i=s_i-1$, $i=2,3,4$, ta có:

$y_1+2y_2+...+4y_4=22$

Ta có:

$y_1+2y_2+...+4y_4=22$

$y_1 \leq 22$, $y_2 \leq 11$, $y_3 \leq 7$, $y_4 \leq 5$

Số bộ nguyên không âm $\left ( y_1,y_2,y_3,y_4 \right )$ chính là hệ số của $x^22$ trong đa thức sau:

$P\left ( x \right )=(1+x^4+...+x^{20})(1+x^3+...+x^{21})(1+x^2+...+x^{22})(1+x+...+x^{22})$

$=\frac{\left ( x^{24}-1 \right )^3(x^{23}-1)}{\left ( x-1 \right )...(x^4-1)}$

$=\frac{(x^{23}-1)(x^{24}-1)(x^{12}+1)^2(x^6+1)(x^2-x+1)(x^8+x^4+1)}{(x-1)^2}$

$=(...+x^{22}-2 x^{21}+4 x^{20}-2 x^{19}+4 x^{18}-2 x^{17}+3 x^{16}-x^{15}+3 x^{14}-2 x^{13}+3 x^{12}-x^{11}+2 x^{10}-x^9+2 x^8-x^7+2 x^6-x^5+x^4+x^2-x+1)(1+2x+3x^2+...)$

$=(...+x^{22}-2 x^{21}+5 x^{20}-2 x^{19}+4 x^{18}-2 x^{17}+3 x^{16}-x^{15}+3 x^{14}-2 x^{13}+3 x^{12}-x^{11}+2 x^{10}-x^9+2 x^8-x^7+2 x^6-x^5+x^4+x^2-x+1)(1+2x+3x^2+...)$

Hệ số $x^{22}$ trong đa thức trên là $1\times 1-2\times 2+5\times 3-2 \times 4+4 \times 5-2 \times 6+3 \times 7-8+3 \times 9-2 \times 10+3 \times 11-12+2\times 13-14+2 \times 15-16+2 \times 17-18+19+21-22+23=136$

Vậy số cách chia kẹo thoả mãn yêu cầu đề bài là $136$

Dùng tỉ số kép trong chứng minh điểm cố định

Đề bài: Cho tam giác ABC, D là điểm cố định trên BC. P là điểm nằm trong tam giác ABC. Gọi $B_1$, $C_1$ lần lượt là hình chiếu của P lên CA, AB. $DB_1, DC_1$ cắt AB, AC tại $C_2, B_2$. Giao điểm khác A của đường tòn ngoại tiếp $AB_1C_1, AB_2C_2$ là Q. Chứng minh rằng PQ luôn đi qua điểm cố định

Lời giải:

Kẻ DE, DF song song AB, AC. đường thẳng qua E, F vuông AC, AB cắt nhau tại I.

Theo tỉ số kép thì $(C_1C_2F)=D(C_1C_2FE)=D(C_2C_1EF)=(B_1B_2E)$

Ngoài ra có phép vị tự quay tâm Q do có $B_1B_2$ cắt $C_1C_2$ tại A và $QAB_1C_1$, $QAB_2C_2$ nội tiếp,

Phép vị tự quay tâm Q biến tam giác $QC_1C_2$ thành tam giác $QB_1B_2$

$QC_1C_2 \sim QB_1B_2$
Do có tỉ số kép nên $QB_2C_2 \sim QEF$

$ \Rightarrow \angle B_2QC_2= \angle EQF= 180^o- \angle FIE$

Vậy QI vuông AQ, mặt khác $PQ \perp AQ$

Vậy I, P, Q thẳng hàng

Nên PQ đi qua I cố định

Ý tưởng đối xứng hóa trong chứng minh bất đẳng thức

Đề bài: (China TST 2006):

Cho x,y,z dương thỏa mãn: $x+y+z=1$. Chứng minh rằng:

$\frac{xy}{\sqrt{xy+yz}}+\frac{yz}{\sqrt{yz+zx}}+\frac{zx}{\sqrt{zx+xy}}\leq \frac{\sqrt{2}}{2}$

Lời giải:



$(\sum \frac{xy}{\sqrt{xy+yz} } ) ^2 \leq (\sum (xy+xz ) )(\frac{x^2y^2}{(xy+yz)(xy+xz)} ) = (2 \sum xy)(\frac{\sum x^2y^2(yz+xz) }{(xy+yz)(xy+xz)(yz+zx)}$

Mà $\frac{\sum x^2y^2(yz+xz) }{(xy+yz)(xy+xz)(yz+zx)}= \frac{\sum xy(x+y) }{(x+y)(y+z)(x+z) } $

Do đó, ta cần chứng minh $(2 \sum xy ).\frac{\sum xy(x+y) }{(x+y)(y+z)(z+x) } \leq \frac{1}{2} $

Đặt $a+b+c=p , ab+bc+ca =q , abc=r $

Chuyển $pqr$, ta cần chứng minh $r(12q-1) \geq 4q^2-q $

TH1: $\frac{1}{4} \leq q \leq \frac{1}{3} $

Khi đó, áp dụng BĐT Schur bậc 3 ta có đpcm.

TH2: $\frac{1}{12} \leq q \leq \frac{1}{4} $ thì ta có đpcm do $VT \geq 0 \geq VP$

TH3: $0 \leq q \leq \frac{1}{12} $ Khi đó, ta có cả 2 vế đều âm

Do đó đổi dấu, ta cần chứng minh $r(1-12q) \leq q-4q^2 $

Hay $r \leq \frac{q-4q^2}{1-12q} $

Mà ta có $pq \geq 9r \Rightarrow r \leq \frac{q}{9} $ ( do $p=1$ )

Khi đó, ta cần chứng minh $\frac{q}{9} \leq \frac{q-4q^2}{1-12q} \Leftrightarrow q \leq \frac{1}{3} $ đúng

Vây ta có đpcm.

Phép vị tự, nghịch đảo và đường thẳng steiner của tứ giác toàn phần

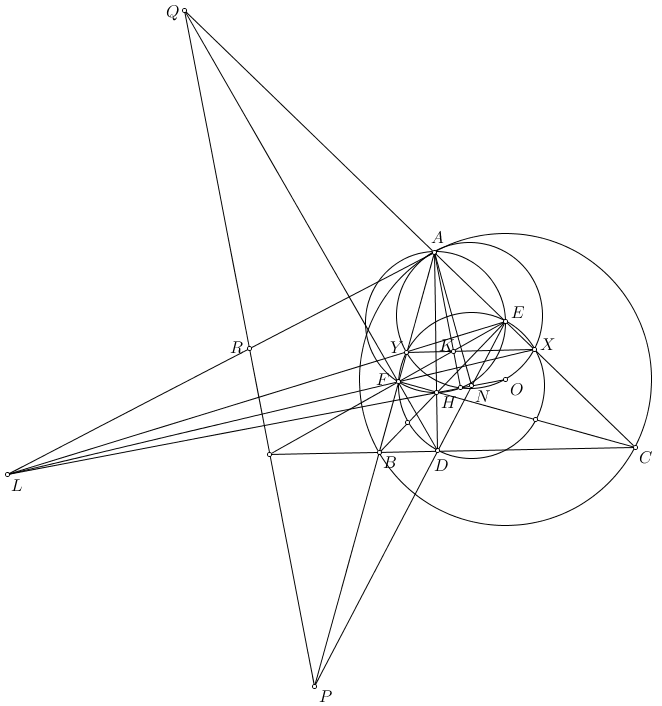
Bài toán: Cho tam giác ABC nội tiếp (O). Đường tròn nội tiếp (I) tiếp xúc BC, CA, AB tại D, E, F. AO cắt (O) tại A'. kẻ DG vuông EF.
a) Chứng minh rằng G, I, A' thẳng hàng.
b) Gọi H là trực tâm của tam giác ABC. Chứng minh: GD là phân giác của $\angle HGI$

Lời giải:

Cách 1: Gọi Ia, Ib, Ic là tâm đường tròn bàng tiếp góc A, B, C.
Ta có IaIbIc và tam giác DEF có các cạnh lần lượt song song với nhau nên tồn tại phép vị tự tâm K biến tam giác này thành tam giác kia.
Ta có I là trực tâm của tam giác IaIbIc, O là tâm đường tròn Euler nên I' đối xứng I qua O là tâm đường tròn ngoại tiếp tam giác đó
Phép vị tự tâm K biến G thành A, I thành I' nên  GI song song AI'.
Mặt khác AII'A' là hình bình hành( do hai đường chéo cắt nhau tại trung điểm mỗi đường)
Nên ta có IA'//I'A
Vậy G, I, A' thẳng hàng
Cách 2: Phép nghịch đảo tâm I phương tích $r^2$ (r là bán kính đường tròn nội tiếp (I) ). biến đường tròn Euler qua G,M thành (O), EF thành (AIEF). vậy biến G thành T là giao của (AIEF) và (O). T thuộc đường tròn đường kính AI nên $ \angle ATI =90^o$ Vậy TGI đi qua A'.
Cách 3: G(DF,BC)=-1 nên GD là phân giác $\angle GBC$,$\Rightarrow \Delta GBF$  ~ $\Delta CGE$, dùng phép vị tự quay tâm T cho ta $ \frac{TE}{TF}=\frac{EC}{FB}=\frac{EG}{FG} $ nên TG là phân giác TFE, I là trung điểm cung EF cho ta điều phải cm
b) Gọi H' đối xứng I qua EF thì H' là trực tâm của tam giác AEF.

Do R là điểm Miquel của tam giác ABC nên đối xứng của R qua EF sẽ thuộc đường thẳng steiner đi qua H' của tam giác AEF, đi qua H của tam giác DEF, nên R' thuộc HH' là đường thẳng steiner của tứ giác toàn phần BCEF. Mặt khác IR cắt trục đối xứng là EF tại T nên R'TH' thẳng hàng.

Suy ra $\angle  FTR'= $\angle ITE$

Bất đẳng thức ba biến không đồng bậc

Đề:
Cho $a,b,c$ là số thực không âm. CMR:$a^3+b^3+c^3+9abc+4(a+b+c)$ $\ge $ $8(ab+bc+ca)$

Giải:



Áp dụng bất đẳng thức AM-GM, ta có

\[a^3+b^3+c^3+9abc+4(a+b+c) \geqslant 4\sqrt{(a^3+b^3+c^3+9abc)(a+b+c)}.\]

Ta quy bài toán về chứng minh

\[(a^3+b^3+c^3+9abc)(a+b+c) \geqslant 4(ab+bc+ca)^2.\]

Bất đẳng thức này có thể chứng minh bằng bất đẳng thức Cauchy-Schwarz và Schur bậc 4 qua p, q, r như sau:

Theo Schur bậc 4 thì: $p^4+4q^2-5p^2q+6rp \ge 0$

Nên ta chỉ cần chứng minh $p^2q+3rp \ge 4q^2$

Khai triển ra ta dùng AM-GM: $a^3b+b^3a \ge 2a^2b^2$ Có điều phải chứng minh.