Cực và đối cực trong bài toán.

Đề: Cho tam giác ABC có I là tâm nội tiếp, Q là tiếp điểm trên AC, E là trung điểm AC. K là trực tâm của tam giác BIC. CM: KQ vuông IE.

Lời giải:

Cách 1: Gọi $F$ là trung điểm $AB$ Gọi $(I)$ tiếp xúc $BC$ tại $P.$ Nếu $BI$ cắt $EF$ tại $L,$ Ta có $\widehat{FLB}=\widehat{LBC}=\widehat{FBL}$ $\Longrightarrow$ $\triangle FBL$ cân tại F $\Longrightarrow$ $FA=FB=FL$ $\Longrightarrow$ $\widehat{ALB}=90^{\circ}$ $\Longrightarrow$ $AQLI$ is cyclic $\Longrightarrow$ $\widehat{CQL}=\widehat{AIL}=90^{\circ}-\tfrac{1}{2}\widehat{ACB}=\widehat{CQP}$ $\Longrightarrow$ $L \in PQ,$ i.e. $L$ nằm trên đường đối cực của $C$ đối với $(I)$, nên C thuộc đường đối cực của L mà $CK \perp IL$ nên CK là đường đối cực của $L$ đối với $(I)$, suy ra đường đối cực của K sẽ là đường thẳng qua L $\Longrightarrow$ $ELF \perp IK$ là đường đối cực của $K$ đối với $(I)$ , ta có Q là đường đối cực của E đối với (I) $\Longrightarrow$  $KQ$ đường đối cực của $E$ đối với $(I)$ $\Longrightarrow$ $KQ \perp IE,$ dpcm.

Cách 2:Gọi$P$ là tiếp điểm của đường tròn bàng tiếp góc B với $AC$. Khi đó $ \angle KIQ=\angle C=\angle BCP$ và \[ \frac{BC}{CP}=\frac{KI}{IQ}. \]
Vì thế $ \triangle CBP \sim \triangle QKI $ và $ \angle IKQ=\angle CBP$ $ \Rightarrow $ $ KQ\perp BP $.

mà $BP\parallel IE$, nên $KQ\perp IE$.

Về phép đếm quay quanh tâm

Ví dụ 1(VMO 2010): Cho bảng 3x3 và n là một số nguyên dương cho trước. Tìm số các cách tô màu không như nhau khi tô mỗi ô bởi 1 trong n màu.
Hai cách tô màu được gọi là như nhau nếu 1 cách nhận được từ cách kia bởi 1 phép quay quanh tâm.
Lời giải:
Cách của thầy Trần Nam Dũng:

Ví dụ 2: (AIME 1996) Hai ô của hình vuông 7 × 7 được tô bằng màu vàng. Các ô còn lại được tô bằng màu đỏ. Hai cách tô đượcc coi là tương đương nhau nếu chúng có thể thu được từ nhau bằng một phép quay trên mặt phẳng của hình vuông. Đếm sô các cách tô màu không tương đương.

Lời giải:
(Xây dựng hệ trục trên hình vuông ô đầu tiên đánh số 1 từ trái sang đánh đến số 7, từ trên xuống đánh từ 1 đến 7)
Ta chia hai ô màu vàng của hình vuông thành 3 loại:

Loại 1: có 1 ô (4;4), thì ô còn lại có 48 cách chọn ( có thể bị lặp). Do các phép quay 90 độ, 180 độ, 270 độ tạo thành những cách khác ta phải loại bớt nên có 48/4=12 cách chọn

Loại 2: các ô có tọa độ là (4,x), (4, 8-x) và (x,4), (8-x, 4) và các ô chéo của hình vuông con ở trong thì khi đó sẽ có 4.3=12 cách chọn như vậy.(Do có 3 hình vuông con mà tâm là (4;4))

Loại 3: Không tính loại 2. Rõ ràng là $\frac{\mathbb{C}_2^{49}-24}{4}$

Tổng cộng có: $\frac{\mathbb{C}_2^{49}-24}{4}+12=300$ cách chọn.
Có thể thấy rõ qua hình sau:

Chú ý: -Có thể không xài loại 1 làm gì nhưng viết vào để cho dễ hình dung.
-Đây là trường hợp của bổ đề Burnside

Ví dụ 3 (tạp chí Kvant số 5 năm 2000): Một đường tròn chia làm p cung bằng nhau. Hỏi có bao nhiêu cách tô các cung bằng a màu. Hai cách tô được gọi là giống nhau nếu có thể thu được từ nhau bởi 1 phép quay.

Với bài toán trên, có $ a^p $ cách tô màu p cung. Trong những số cách ấy, có những cách ta đếm lặp, cần loại đi. Ta thấy rằng nếu p cung được tô bởi 1 màu thì khi quay các góc 2pi/p, 4pi/p,..., 2(p-1)pi/p không thu được những cách tô khác. (ta có thể chứng minh rằng nếu $n \vdots k$ khi đó tồn tại phép quay góc 2kpi/p biến đường tròn này thành đường tròn kia) . Trong khi đó, những cách tô sử dụng 2 màu trở lên khi quay sẽ cho ra các cách tô khác (chú ý tính nguyên tố của p). Vì vậy, mỗi một cách tô sử dụng 1 màu (có a cách tô như vậy) chỉ được đếm 1 lần trong tổng $a^p $cách tô, trong khi đó mỗi cách tô sử dụng 2 màu trở lên (có $a^p - a$ cách tô như vậy) được đếm p lần trong tổng nói trên.

Từ đó suy ra số cách tô cần tìm bằng $ a + \dfrac{a^p-a}{p} $.

Chú ý: Từ kết quả này có thể suy ra định lí Fermat nhỏ.

Chứng minh tồn tại số tự nhiên thỏa mãn yêu cầu bài toán

Bài toán:

Cho trước $ k\in \mathbb{Z}^+$ và $ m$ lẻ .

Chứng minh rằng tồn tại $ n\in \mathbb{Z}^+$ sao cho $ 2^k| n^n-m$

Lời giải:

Ta sẽ chứng minh quy nạp theo $ k$.

Trường hợp $ k=1$ là hiển nhiên, chọn $ n=1$.

Giả sử rằng tồn tại $ n$ sao cho $ 2^k|n^n-m$,Đặt $ n=n_0$ hay $ 2^k|n_0^{n_0}-m$ hiển nhiên $ n_0$ lẻ

Tiếp theo xét 2 trường hợp

$ 1)$ Nếu $ 2^{k+1} | n_0^{n_0}-m$

Rõ ràng chỉ cần chọn $ n=n_0$.

$ 2)$ Nếu $ 2^{k+1}$ Không là ước của $ n_0^{n_0}-m$.

Đặt $ n_0^{n_0}-m=u\cdot 2^k$ Với $ u$ lẻ và theo định lý Euler,Cho mọi số lẻ $ a$ ta có $ a^{2^{k}}\equiv 1\pmod{2^{k+1}}$,Vì thế

$ (2^k+n_0)^{2^k+n_0}-m=(2^k+n_0)^{2^k}\cdot (2^k+n_0)^{n_0}-m\equiv (2^k+n_0)^{n_0}-m\\\equiv n_0^{n_0}+n_0\cdot n_0^{n_0-1}\cdot 2^k-m=(u+n_0^{n_0})2^k\equiv 0\pmod{2^{k+1}}$ Vì cả $ u$ và $ n_0$ đều lẻ.

Vì thế $ n=2^k+n_0$ thỏa mãn, nên ta có đpcm

Dùng hàng điểm điều hòa để chứng minh đồng quy

Đề bài:

Cho tam giác ABC không đều trực tâm H, tâm đường tròn ngoại tiếp O,đường cao AD. Gọi E là giao điểm của OA với BC. 1 đường thẳng $\Delta$ đi qua D và song song với đường thẳng Euler của tam giác cắt AB,AC lần lượt tại M,N. I là trung điểm của AE. DI cắt AB ,AC lần lượt tại P,Q.Chứng minh rằng MQ,NP,OD đồng quy biết MQ cắt NP tại T.

Lời giải:

Gọi BB', CC' là 2 đường cao của tam giác ABC. B'C' cắt AD tại J. Ta có (A, H, J, D) = -1.

Gọi K là giao điểm của MN và AO
AO cắt (O) tại điểm thứ 2 là G. Ta có tam giác AB'C' đồng dạng tam giác ABC nên phép vị tự quay tâm A biến J thành H, E thành G. Dễ dàng suy ra JE//HG

Vậy ta có hệ thức $\frac{AJ}{AH}=\frac{AE}{AG}=\frac{AI}{AO}$

Hay JI song song với HO, hay JI song song với DK.

Do đó (A, O, I, K) = -1.

Vậy D(A, O, I, K) = -1, từ đó có MQ, NP, OD đồng quy ( bằng cách gọi giao điểm của OD và AB, AC).

Phép nghịch đảo để chứng minh thẳng hàng

Bài toán: Gọi $ H,O$ là trực tâm và tâm ngoại tiếp $ \Delta ABC$. Đường tròn ngoại tiếp và đường tròn Euler của $ \Delta HBC$ cắt nhau tại $ \{M,N \}$. Gọi $ O^*$ là tâm đường tròn ngoại tiếp $ \Delta AMN$ và $ L$ là trung điểm của $ OA$. Chứng minh rằng $ H,O^*,L$ thẳng hàng            

Lời giải:

Gọi    $ A’,B’,C’$ là chân đường cao đến các cạnh $ BC,CA,AB.$ $ F$ là trung điểm $ BC$  Gọi $ B’C’$ cắt $ BC$ tại $ P$ và cắt $ (O)$ tại $ B’',C’'.$ Vì $ (B,C,A’,P) =- 1,$ nên  $ PB \cdot PC = PA’ \cdot PF$ $ \Longrightarrow$ $ PB’' \cdot PC’' = PA’ \cdot PF$ $ \Longrightarrow$ $ F \in \odot(A’B’'C’').$ Vì thế tâm của $ \odot(A’B’'C’')$ là đường thẳng qua vuông góc từ $ A$ đến $ B’C’$ giao với trung trực $ A’F,$ chính là trung điểm $ L$ của $ AO.$ Phép nghịch đảo $ \mathcal{I}$ tâm $ H,$ biến $ (O)$ thành đường tròn chín điểm $ \mathcal{N},$ và biến $ B’C’$ thành đường tròn ngoại tiếp $ \triangle HBC$ và $ \odot(A’B’'C’')$ thành đường tròn đi qua $ A$ và Giao điểm $M,N$ của $ \mathcal{N}$ và $ \odot(HBC),$ Là ảnh của $ A’,C’',B’'$ $ \Longrightarrow$ phép nghịch đảo tâm $ H,$ biến tâm ngoại tiếp $ L$ của $\odot (A’B’'C’')$ và tâm $ O^*$ của tam giác $ \odot(AMN)$ thẳng hàng.

Ứng dụng bổ đề ERIQ

Bài toán 1: Tam giác ABC không cân $\Delta ABC$. $E,F$ là các chân đường cao từ $B,C$ trên $AC,AB$, H là trực tâm
$E,Q$ trên $[FB);[EC)$ sao cho: $FP=FC; EQ=EB$
$BQ$ cắt $CP$ tại $K$.
$I,J$ là trung điểm của $BQ,CP$.
$IJ$ cắt $BC,PQ$ tại $M,N$
1/ Chứng minh: $HK\bot IJ$
2/ $\widehat{PAM}=\widehat{QAN}$

Lời giải:

Ta có $\overline{HF}.\overline{HC}=\overline{HE}.\overline{HE}$
Nên $H$ thuộc trục đẳng phương của $[CP]$ và $[BQ]$
$BCQP$ là tứ giác nội tiếp nên $\overline{KC}.\overline{KP}=\overline{KB}.\overline{KQ}$
Vì thế $K$ thuộc trục đẳng phương $[CP]$ và $[BQ]$
Vậy $HK\perp IJ$
(b)
Ta có $\dfrac{\overline{IQ}}{\overline{IB}}=\frac{\overline{JP}}{\overline{JC}}$
Áp dụng bổ đề ERIQ được: $\dfrac{\overline{BM}}{\overline{MC}}=\dfrac{\overline{QN}}{\overline{NP}}\Rightarrow đpcm$



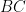Bài toán 2 (Juliel blog) : Cho tứ giác nội tiếp được đường tròn. Gọi lần lượt là các giao điểm của và , và 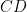. Gọi là giao điểm của phân giác hai góc 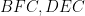. lần lượt là trung điểm của . Chứng minh rằng thẳng hàng.

Lời giải :



Gọi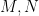 lần lượt là giao điểm của với .

Ta sẽ chứng minh .

Thật vậy, ta có



Mà trong tam giác thì cũng là phân giác, do đó nó cũng là trung tuyến, hay .

Theo tính chất phân giác :



Mà theo hệ thức lượng trong đường tròn thì

Suy ra

Xét hai bộ ba điểm thẳng hàng các điểm lần lượt thuộc và thỏa mãn (chứng minh trên)

Các điểm lần lượt thuộc và thỏa

Như vậy theo bổ đề ta có thẳng hàng. Đây là điều phải chứng minh.

Dùng hàng điểm điều hòa để chứng minh vuông góc.

Bài toán: Cho tam giác ABC, đường cao BE, CD. gọi F, G là hình chiếu của D, E trên BC. DG cắt EF tại M. Chứng minh rằng AM vuông BC.

Lời giải:

Gọi P, Q là hình chiếu của A, M trên BC.
$U \equiv MQ \cap DE,$  $V \equiv AP  \cap DE$ và $L \equiv DE \cap BC.$

Vì $EG \parallel DF,$ theo bổ đề hình thang  $M(D,E,U,L)=-1,$ nhưng $(D,E,V,L)=-1$ vậy ta có đpcm

TÍNH CHẴN LẺ TRONG BÀI TOÁN TỔ HỢP

Tính chẵn lẻ là một trong các bất biến quan trọng nhất trong một số tình huống tổ hợp. Đó là một ý tưởng đơn giản nhưng vô cùng hiệu quả. Tính chẵn lẻ là việc xét đồng dư theo modulo 2, một cách phức tạp hơn ta có thể nghĩ đến một lớp đồng dư theo modulo là một số tự nhiên tùy ý như một bất biến trong một số bài toán.
 VD1: Có 2015 bánh răng được xếp trên một mặt phẳng kề nhau tạo thành một vòng kín. Hỏi các bánh răng có thể quay cùng lúc hay không?
Lời giải: Câu trả lời là không. Mấu chốt ở bài này là việc phát hiện ra hai bánh răng kề nhau luôn quay ngược nhau. Giả sử bánh răng thứ nhất quay theo chiều dương kéo theo bánh thứ hai quay chiều âm, bánh thứ ba quay chiều dương... Như vậy bánh có số thứ tự lẻ quay chiều dương còn bánh có thứ tự chẵn quay chiều âm. Do đó bánh số 1 và số thứ 2015 cùng quay chiều dương. Vô lý. Ý tưởng chính của bài toán trên là sự xen kẽ chiều quay của các bánh răng. Tìm đối tượng xen kẽ cũng là hướng đi đầu tiên của các bài toán sau.
VD2:Trong một bàn cờ vua , một quân mã bắt đầu đi từ vị trí a1 và trở lại đó sau một số bước đi. Chứng minh số bước đi vừa thực hiện là một số chẵn.
Lời giải: Vị trí ban đầu của con mã là màu đen. Sau bước đi thứ nhất nó đến ô màu trắng, sau bước thứ hai nó đến ô màu đen.... Như vậy sau lẻ bước nó đến ô trắng và sau chẵn bước nó đến ô đen. Suy ra đpcm.
 VD3: Một đường gấp khúc khép kín được tạo bởi 11 đoạn thẳng nằm trên một mặt phẳng. Tồn tại hay không một đường thẳng d không đi qua bất kỳ đầu mút nào của các đoạn thẳng trên và cắt tất cả 11 đoạn thẳng đó.
Lời giải:
Gọi $(P_1), (P_2)$ là hai nửa mặt phẳng có bờ là đt d. Kí hiệu đường gấp khúc trên là $A_1A_2A_3...A_{11}A_1$ . Giả sử $A_1$ thuộc $(P_1)$ thì $A_2$ thuộc $(P_2)$, $A_3$ thuộc $(P_1)$,...,$A_{11}$ thuộc $(P_1)$. Nhưng khi đó $A_1$ và $A_{11}$ cùng thuộc $(P_1)$ nên d không thể cắt đoạn $A_1A_{11 }$điều này trái với giả thiết nên không thể tồn tại đường thẳng d thỏa mãn.
VD4 Ba quả bóng hockey A, B, C nằm trên một sân chơi. Một người đánh một trong ba quả đó sao cho nó đi qua giữa hai quả còn lại. Anh ta làm thể 25 lần. Liệu anh ta có thể đưa ba quả bóng trở về vị trí ban đầu hay không?
Lời giải:

Giả sử ban đầu ba quả bóng được sắp thứ tự theo chiều dương. Sau mỗi lượt chơi thì thứ tự của chúng thay đổi từ dương sang âm và ngược lại. Do vậy sau lượt đánh thứ nhất thứ tự của chúng theo chiều âm, sau lượt thứ hai lại đổi thành chiều dương,...Sau 25 lượt thì thứ tự của 3 quả bóng đó là chiều âm, do đó anh ta không thể đưa chúng về vị trí ban đầu.
VD5: Có hay không một đường gấp khúc khép kín gồm 9 đoạn thẳng sao cho mỗi đoạn cắt duy nhất một trong các đoạn còn lại?
Lời giải:
Nếu tồn tại đường gấp khúc đó thì tập hợp các đoạn thẳng trên có thể chia thành từng cặp các đoạn thẳng giao nhau. Như vậy tổng số đoạn thẳng phải là số chẵn.
Nhận xét: Điểm mấu chốt của ví dụ trên là nếu một nhóm các đối tượng có thể chia thành từng cặp thì số các đối tượng là một số chẵn. Sau đây là một số ví dụ tương tự.
VD6: Có thể chia một đa giác lồi 13 cạnh thành các hình bình hành được không?
Lời giải:
Giả sử thực hiện được công việc trên. Khi đó cạnh A1A2 phải thuộc một hình bình hành A1PNM trong đó A1P thuộc A1A2. Tiếp đó tồn tại hình bình hành RSPQ trong đó P,Q thuộc MN... Quá trình này cứ tiếp tục đến khi tồn tại một hình bình hành có cạnh song song với A1 A2 và thuộc một cạnh AmAm+1 nào đó và cạnh Am Am+1 tương ứng với A1A2 là duy nhất. Như vậy các cạnh của đa giác được chia thành các cặp nên số cạnh phải là số chẵn . Vô lý. Tương tự ta giải quyết các bài toán sau nhờ kỹ thuật “ghép cặp”
VD7: 25 quân cờ được đặt trên bàn cờ 25x25 sao cho mỗi quân cờ đối xứng với một quân cờ khác qua một đường chéo. Chứng minh có ít nhất một quân cờ được đặt trên một đường chéo.
VD8: Cho một bảng 15x15 ta viết các số từ 1 đến 15 sao cho hai ô đối xứng với nhau qua một trong hai đường chéo chính thì chứa hai số bằng nhau và không có số nào trong cùng một hàng hoặc một cột bằng nhau. Chứng tỏ rằng không có hai số nào trên đường chéo chính bằng nhau.
VD9: Hình vuông “kỳ diệu” là một bảng vuông 6x6 với mỗi một con số ở mỗi ô sao cho tổng các số ở mỗi cột, mỗi hàng và hai đường chéo bằng nhau . Có thể lập ra một hình vuông “kỳ diệu” từ 36 số nguyên tố đầu tiên không?
Lời giải:
Không . Vì khi đó tổng các số thuộc hình vuông là một số chẵn trong khi đó tổng của 36 số nguyên tố đầu tiên lại là số lẻ.
VD10: Các số từ 1 đến 10 được viết trên bảng theo một hàng ngang theo một thứ tự bất kỳ. Liệu có thể chèn vào giữa tất cả hai số kề nhau một cách tùy ý dấu “+” hoặc dấu “-” sao cho kết quả cuối cùng nhận được là số 0 hay không?
Lời giải: Giả sử ban đầu các dấu gồm toàn dấu “+” sau đó ta thay một số dấu cộng bằng dấu trừ. Bất biến ở đây là tính chẵn lẻ của tổng 10 số đó không đổi. Nhưng tổng các số từ 1 đến 10 là số lẻ nên sau hữu hạn bước không thể đưa về tình huống đề bài yêu cầu.
VD11: Một con châu chấu nhảy trên một đường thẳng. Bước đầu tiên của nó dài 1 cm, bước thứ hai dài 2cm và cứ thế, mỗi bước nó có thể nhảy về bên trái hoặc bên phải. Hỏi sau 2015 bước nó có thể trở về vị trí ban đầu hay không ?
Câu trả lời là không.
VD 12: Trên bảng có các số 1;2;3;...;2013. Một học sinh xóa hai số bất kỳ và thay bằng giá trị tuyệt đối của hiệu hai số đó. Sau hữu hạn bước chỉ còn một số trên bảng. Số này có thể abừng 0 được không?
Lời giải: Ta có (a + b) - |a - b| là số chẵn với hai số tự nhiên a, b bất kỳ. Như vậy tổng cac số sau mỗi bước luôn cùng tính chẵn lẻ. Do đó số cuối cùng phải là số lẻ vì tổng các số ban đầu là lẻ.
VD 13:
Có 45 điểm cùng nằm trên một đường thẳng AB, tất cả đều nằm ngoài đoạn AB. Chứng minh tổng khoảng cách tổng các khoảng cách từ các điểm này tới A khác tổng các khoảng cách từ các điểm đó tới B.
Lời giải:
Nhận thấy hiệu hai tổng khoảng cách đó luôn bằng số lẻ lần độ dài đoạn thẳng AB nên ta có đpcm.

Bản chất của bất biến xét theo tính chẵn lẻ là xét theo modul 2. Ta có thể tổng quát khi thay 2 bởi một số tự nhiên khác.  
VD14: Cho 1000 số từ 1 đến một 1000 được viết theo một hàng ngang trên bảng. Mỗi lần ta thay một hoặc vài số trên bảng bởi tổng các chữ số của nó. Hỏi dãy số cuối cùng thu được có nhiều số 1 hơn hay nhiều số 2 hơn?

Lời giải:
Trong dãy số trên có 112 số chia 9 dư 1 và 111 số chia 9 dư 2. Vậy dãy số cuối cùng có số 1 nhiều hơn số 2.
Nhận xét:  Đại lượng bất biến ở đây là một số tự nhiên và tổng các chữ số của nó có cùng số dư trong phép chia cho 9
VD15: Mối bước cho phép chọn một số tự nhiên a và phân tích a thành tích hai số tự nhiên m, n sau đó viết lên bảng hai trong số bốn số m ± 2, n ± 2. Ban đầu ta có số a = 20152015...2015 (100 số 2015). Hỏi sau một số bước như vậy có thu được một dãy gồm toàn số 1 hay không?
Lời giải:
Vì a chia 4 dư 3 nên trong hai số m, n phải có một số chia 4 dư 1 và một số chia 4 dư 3.Mà số chia 4 dư 1 thì cộng 2 hay trừ đi 2 đều chia 4 dư 3. Do đó ở mỗi bước luôn có mặt số chia 4 dư 3, như vậy sau hữu hạn bước không thể ra kết quả như đề yêu cầu.
Nhận xét: Bài này ta để ý đến a là một số chia 4 dư 3 cũng như việc tồn tại các số như vậy trong dãy.
VD16:Trên bảng có hai số 1 và 2. Thực hiện việc ghi số theo nguyên tắc sau: Nếu trên bảng có hai số a, b thì được phép ghi thêm số c = a + b + ab. Hỏi bằng cách đó có thể xuất hiện các số 2013, 2014 và 2015 được không?
Lời giải:
Dãy các số được viết là: 1; 2; 5; 11; 17;... Dễ thấy các số viết thêm trong dãy trên đều chia 3 dư 2. Như vậy bất biến trên cho phép ta khẳng định số 2013 và 2014 không thể có mặt. Với số 2015 ta phải dùng bất biến khác.
Đem tăng thêm 1 cho mỗi số hạng ở dãy trên thì ta nhận được dãy: 2; 3; 6; 12; 18;... Ta chứng minh cho các số hạng của dãy đều có dạng 2m.3n nhưng số 2015 + 1 không có tính chất đó.
VD17: Có ba đống sỏi với số lượng tương ứng là 8; 9; 19 viên. Ta được phép chọn hai đống sỏi và chuyển một viên của mỗi đống đã chọn sang đống còn lại. Hỏi sau một số lần làm như vậy ta có thể thu được ba đống sỏi mỗi đống có đúng 12 viên không?
Lời giải:
Bất biến trong bài này là trong tất cả các trạng thái thì số dư của số sỏi trong mối đống trong phép chia cho 3 là một hoán vị của bộ {0;1;2}. Do đó không thể thưch hiện được.

Tương tự ta có bài sau:

VD18: Ngoài biển đông, trên một hòn đảo sinh sống ba giống thằn lằn có ba loại màu: màuxám có 133 con, màu nâu có 155 con và màu đỏ có 177 con. Nếu hai con thằn lằn khác màu gặp nhau thì chúng đồng thời đổi sang màu thứ ba (ví dụ nếu thằn lằn màu xám gặp thằn lằn màu nâu thì cả hai con đều đổi sang màu đỏ). Trong những trường hợp hai con thằn lằn cùng màu gặp nhau thì chúng giữ nguyên không đổi màu. Có xảy ra tình trạng là trên đảo tất cả thằn lằn cùng một màu được không?
VD19: A và B tiến hành trò chơi với 2014 hạt gạo. Một nước đi là lấy khỏi đống gạo đó 1;2 hoặc 3 hạt. A đi trước và thay phiên nhau. Người nào lấy được hạt gạo sau cùng sẽ là người chiến thắng. Ai là người có thể luôn chiến thắng và chiến thuật ra sao?
Lời giải:
A sẽ là người luôn chiến thắng nếu chới theo chiến thuật sau: Bước 1: A lấy 2 hạt gạo. Bước 2: B lấy x hạt (x = 1;2;3) 7 Bước 3: A lấy 4 – x hạt Cứ tiếp tục như vậy....Ta thấy sau mối lần A lấy thì số gạo còn lại luôn là bội của 4. Ở bước áp chót số gạo còn lại là 4 hạt thì dù B có chọn cách chơi nào thì A cũng là người thắng cuộc.  
VD20: Có một tờ giấy được cắt thành 6 mảnh hoặc 11 mảnh. Sau đó mỗi mảnh bất kỳ trong số đó lại được cắt thành 6 hoặc 11 mảnh nhỏ hơn. Hỏi có thể tạo thành 2015 mảnh không?
Lời giải:
Sau mỗi lần cắt một mảnh giấy thành 6 mảnh hoặc 11 mảnh thì số mảnh giấy tăng lên là 5 hoặc 10. Như vậy tính bất biến của bài toán là “số mảnh giấy luôn tăng lên một bội số của 5”. Vậy số mảnh giấy sau các lần cắt có dạng 1 + 5k, mặt khác 2005 có dạng 5k nên với cách cắt như trên, từ một tờ giấy ban đầu, ta không thể cắt được thành 2005 mảnh. Nhận xét. Bất biến của bài toán là số mảnh giấy tăng lên luôn là một bội số của 5.
VD21: Trên bảng, người ta viết các số tự nhiên liên tiếp từ 1 đến 100 sau đó thực hiện trò chơi như sau: mỗi lần xóa hai số bất kỳ và viết một số mới bằng tổng lập phương của hai số đã cho. Việc làm này thực hiện liên tục cho đến khi còn một số trên bảng. Hỏi số cuối cùng còn lại trên bảng có thể là $987654321^n$ (n là số tự nhiên lớn hơn 1) hay không? Tại sao?
Lời giải:
Để ý rằng : $(a^3 + b^3 ) – (a + b) = (a^3 - a) + (b^3 - b )$ luôn chia hết cho 3 với mọi cặp số tự nhiên a, b. Do đó sau mỗi lần chơi tổng các số ban đầu thay đổi một lượng là bội của 3. Vì tổng các số từ 1 đến 100 chia cho 3 dư 1 nên ở trạng thái kết thúc ta cũng phải thu được số chia 3 dư 1, nhưng số đề cho lại là số chia hết cho 3.
Ta cùng luyện tập thêm một số bài cùng chủ đề sau:
Bài 1: Một con ốc sên bò trên một mặt phẳng với vận tốc không đổi. Sau mỗi 15 phút thì nó lại rẽ theo một góc vuông. Chứng minh ốc sên có thể quay lại điểm xuất phát sau một số nguyên lần.
Lời giải:
hi con ốc sên quay trở lại vị trí xuất phát thì nó đã đi được một đường gấp khúc khép kín. Kí hiệu: $\overrightarrow{a},\overrightarrow{-a},\overrightarrow{b},\overrightarrow{-b}$
chỉ các hướng đi lên, đi xuống, sang trái, sang phải của ốc sên. Gọi m, n, p,q là số lần đi lên , xuống, sang trái, sang phải. Ta cần chứng minh (m + n + p + q) là bội của 4.
Từ  $m\overrightarrow{a}+n \overrightarrow{-a}+p \overrightarrow{b}+q\overrightarrow{-b}=0$ mà hai véc to a,b khác phương  nên suy ra m = n và p = q. Do cứ sau 15 phút ốc sên lại rẽ sang góc $90^o$ nên m + n = p + q. Từ đó ta được đpcm
Bài 2: Ba con châu chấu chơi trò nhảy cóc trên một đường thẳng. Cứ mỗi nước đi một con châu chấu nhảy qua một con khác nhưng không nhảy qua hai con. Chúng có thể trở về vị trí ban đầu sau 2n + 1 bước không?
Lời giải:
Sau mỗi lần nhảy thì luôn có một con giữ nguyên vị trí. Sau số chẵn lần nhảy thì có 0 hoặc 3 con cùng đúng vị trí ban đầu. Nhưng 2n + 1 là số lẻ lần không thể thực hiện được.
Bài 3: Một số tự nhiên gồm 17 chữ số. Một học sinh đảo ngược thứ tự các chữ số của số đó rồi đem cộng với số ban đầu. Chứng minh tổng tạo thành có ít nhất một chữ số chẵn.
 Giải:
Gọi số đó là:
$A=\overline{a_1a_2..a_{17}}, B=\overline{a_{17}..a_1a_2}, C=A+B$
Đặt: $x_i=a_i+a_{18-i}$. Xét dãy:
$x_1x_2..x_8x_9x_8x_7..x_1$
Giả sử các chữ số của C gồm toàn số lẻ.Cộng theo hàng dọc ta thấy: x9 chẵn nên x8 phải nhớ 1 sang suy ra: x7 chẵn, x6 nhớ 1 sang, x5 chẵn,..., x1 chẵn. Do đó chữ số đơn vị của C là chẵn. Mâu thuẫn.
Bài 4: Có 100 người lính trong một doanh trại. Mỗi tối 3 người trong số họ có ca trực. Hỏi có thể xảy ra tình huống sau một khoảng thời gian nào đó mỗi người đều trực với tất cả những người còn lại đúng một lần hay không?
Lời giải: Giả sử có thể xảy ra tình huống trên. Xét một người lính A nào đó, từ gt suy ra số người còn lại sẽ được phân hoạch thành các cặp trực cùng A. Nhưng khi đó suy ra tổng số lính của doanh trại phải là số lẻ. Vô lý.
Bài 5: Có 9 số được đặt trên một vòng tròn gồm 4 số 1 và 5 số 0. Mỗi hành động sau được coi là một bước: Ta thêm số 0 vào giữa hai số cạnh nhau nếu hai số đó khác nhau, trường hợp ngược lại ta thêm số 1. Hai số cũ sau đó bị xóa. Hỏi sau một số bước đi các số còn lại có thể bằng nhau được hay không?
Bài 6: Có 25 bạn nam và 25 bạn nữ ngồi quanh một bàn tròn. Chứng minh tồn tại một bạn có cả hai “hàng xóm” là nam. (Tương tự có một bạn có hai hàng xóm đều là nữ).
Lời giải
Kí hiệu 25 bạn nam là N1, N2, ..., N25. Gọi x1, x2,..., x25 là số bạn nữ ngồi giữa hai bạn nam (Ni, Ni+1) với N1 = N26. Ta có: x1+ x2+...+ x25 = 25. (1) Nếu tồn tại xi = 1 thì bài toán được chứng minh. Trường hợp ngược lại: Từ (1) có ít nhất 13 số xi bằng 0. Nếu x1 = x25 = 0 thì N25 chính là người cần tìm. Nếu x1, x25 không đồng thời bằng 0 thì theo nguyên lý Diricle sẽ có một cặp xj = xj+1 = 0 khi đó Nj+1 là người cần tìm.
Bài 7: Hai người chơi cờ. Sau mỗi ván người thắng được 2 điểm, người thua được 0 điểm, nếu hòa thì mỗi người được 1 điểm. Hỏi sau một số ván cờ liệu có 10 xảy ra tình huống một người được 10 điểm, một người được 13 điểm hay không?
Lời giải:
Câu trả lời ở đây là không. Bất biến là tính chẵn lẻ của tổng số điểm của hai người chơi là không đổi.
Bài 8: Trên mặt bàn có 2017 viên bi gồm 667 viên xanh, 669 viên đỏ và 671 viên vàng. Thực hiện thuật toán như sau: Mỗi lần lấy đi hai viên bi khác màu và đặt thêm hai viên bi có màu còn lại. Hỏi có nhận được trạng thái tất cả các viên bi trên bàn có cùng một màu được không?
Lời giải:
Kí hiệu X(n), Đ(n), V(n) tương ứng với số bi màu xanh, đỏ, vàng sau bước đi thứ n. Như vậy X(0) = 667, Đ(0) = 669 , V(0) = 671. Từ thuật toán đề ra ta thấy bất biến ở đây là số dư của các hiệu X(n) – Đ(n), Đ(n) – V(n), V(n) – X(n) không đổi trong phép chia cho 3. Xuất phát từ trạng thái ban đầu ta có các số dư này là 1;2;1. Nhưng ở trạng thái kết thức số bi của ba loại trên là một hoán vị của {0;0;2007} nên không thể thực hiện được.
Bài 9 Trong dãy 1, 9, 9, 9, 8, . . . , mỗi chữ số bắt đầu từ chữ số thứ năm bằng chữ số hàng đơn vị của tổng bốn chữ số liền trước nó. Hỏi trong dãy này có gặp các bộ 1234 và 5678 không?
Lời giải:
Ta thay mỗi chữ số của dãy đã cho bằng số 0 nếu nó là số chẵn và bằng số 1 nếu nó là số lẻ. Ta nhận được dãy số 111101111011110..., trong đó cứ sau bốn chữ số 1 có một chữ số 0 và cứ sau mỗi số 0 có bốn chữ số 1. Các bộ số 1234 và 5678 ứng với các bộ 4 chữ số 1010 và 1001 nên không thể có mặt trong dãy số đã cho.

Tài liệu tham khảo
 1) Mathematical – Circles – Russian Experience
 2) Giải toán bằng đại lượng bất biến – Nguyễn Hữu Điển
 3) Một số chuyên đề trên mạng

Bài toán trò chơi

Bài toán:
Trên bảng viết n ( $n\geq 4$) số nguyên dương liên tiếp. Hai người A và B lần lượt chọn một số từ n số đã cho và xóa số đó đi và thực hiện đến khi trên bảng còn lại 2 số a,b. Biết rằng A thắng cuộc nếu gcd(a,b)=1, B thắng cuộc nếu gcd(a,b)>1. Ai là người thắng cuộc nếu A đi trước :

a) n=2017

b) n là một số nguyên dương không nhỏ hơn 2016

Lời giải:

Trường hợp tổng quát cho $n>8$: Nếu $n$ lẻ, đặt $n=2k+1$. Chiến thuật giúp $A$ thắng: đầu tiên $A$ sẽ loại $n$ ra khỏi bảng và chia $n-1$ số còn lại thành $k$ cặp $(1,2),(3,4),...,(2k-1,2k)$.Mỗi lượt $B$ sẽ chọn $1$ số trong $1$ cặp bất kì, $A$ chỉ việc loại số còn lại trong cặp đó và trên bảng luôn còn những cặp số liên tiếp nên cuối cùng trên bảng sẽ còn $2$ số liên tiếp và $A$ sẽ thắng. Còn nếu $n$ chẵn thì $B$ sẽ thắng: Đặt $n=2k$ gọi $S_i$ là hiệu giữa số số chẵn với số số lẻ trên bảng sau bước thứ $i$ của $B$. Có $S_0=0$, chiến thuật thắng của $B$ như sau: Rõ ràng trò chơi sẽ kết thúc sau $k-1$ bước, trong $k-2$ bước đầu của $B$, anh ta sẽ chọn ra $2$ số lẻ $m,n$ với $(m,n)>1$ (luôn chọn được vì $n>8$) và sẽ chỉ loại những số lẻ trên bảng khác $m,n$ nếu có thể. Nếu trong $k-2$ bước đầu của $A$, $A$ chọn loại $1$ số lẻ tại bước thứ $i$ và $B$ chọn loại $1$ số lẻ khác thì $S_i\geq 2$. Lúc đó $B$ sẽ chọn loại tất cả các số lẻ khác trên bảng và $S_i$ sẽ không giảm. Cuối cùng trên bảng còn ít nhất $2$ số chẵn, $A$ và $B$ cứ loại dần đến khi chỉ còn $2$ số chẵn và $B$ thắng. Còn nếu $A$ luôn chọn loại số chẵn trong $k-2$ bước đầu thì sau $k-2$ bước của cả $2$, trên bảng còn $2$ số chẵn $a,b$ và $2$ số lẻ $m,n$. Nếu sau đó $A$ chọn loại $1$ số trong cặp $(a,b)$ thì $B$ sẽ loại số còn lại trong nhóm đó và trên bảng còn $2$ số $m,n$ với $(m,n)>1$. Còn nếu $A$ chọn loại $1$ số trong $(m,n)$ thì $B$ loại số còn lại, trên bảng còn $2$ số $a,b$ chẵn có $(a,b)>1$. Tóm lại $A$ thắng nếu $n$ lẻ, $B$ thắng nếu $n$ chẵn

Dùng cấp để tìm các số thỏa mãn bài toán

Đề bài: Tìm $p,q$ nguyên tố sao cho $2^{p}+2^{q}\vdots (pq).$

Lời giải:

Dễ thấy $(p,q)=(2,2),(3,2),(2,3)$.

Nếu $p,q \ge 3$. Dùng định lý Fermat nhỏ, ta có $2^{p} \equiv 2 \pmod{p}$. Vì thế $p|2^{q-1}+1$. Ta được $2^{q-1} \equiv -1 \pmod{p}$.

Đặt $q-1=2^x \cdot y$ với $x,y \in \mathbb{N}^*, \; \gcd(y,2)=1$ và đặt $2^y=k$, ta được $2^{q-1}=(2^y)^{2^x} \equiv -1 \pmod{p} \Rightarrow k^{2^{x+1}} \equiv 1 \pmod{p}$.

Ta có $\text{ord}_p(k) |2^{x+1}$.

Vì $k^{2^x} \equiv -1 \pmod{p}$ nên $p \nmid k^{2^x}$. Vì thế $\text{ord}_p(k) \nmid 2^x$. 

Vậy $\text{ord}_p(k)=2^{x+1}$. 

Ta cũng có $2^{p-1} \equiv 1 \pmod{p}$. Nên $2^{x+1}|p-1$. Đặt $p=2^{u} \cdot l+1$ với $u,l \in \mathbb{N}^*, \; \gcd (l,2)=1$ thì $u \ge x+1$.

Tương tự ta cũng được $x \ge u+1$, mâu thuẫn

Vậy câu trả lời là $\boxed{ (x,y)=(2,2),(3,2),(2,3) $

Bài tập tương tự: Tìm $p,q$ nguyên tố sao cho $5^p+5^q \vdots pq$ ( lưu ý là phải xét thêm $p,q =2$)

Hai tiêu chuẩn Eisentein mở rộng

Tiêu chuẩn mở rộng 1: Cho đa thức $P(x)=\sum_{i=0}^{n}a_ix^i$ là một đa thức hệ số nguyên. Nếu tồn tại số nguyên tố p thỏa mãn những điều kiện sau:
i) $ a_n$ không chia hết cho p
ii)  Các hệ số $a_0, a_1, .. a_{n-k}$ chia hết cho p
iii) $a_0$ không chia hết $p^2$.

Chứng minh rằng đa thức $P(x)$ không có ước là $G(x)$ mà bậc của G lớn hơn hoặc bằng k.

Chứng minh:

Giả sử ngược lại: $P(x)=f(x)g(x)$ với: $f(x)=\sum_{i=0}^{r}b_ix^i, g(x)=\sum_{i=0}^{s}c_ix^i, r+s=n, r,s \ge k$. Và do $r+s=n$ và $r,s \ge k$ suy ra $r, s \le n-k$
Dễ thấy rằng $a_0=b_0c_0$ mà $a_0 \vdots p$ và $a_0 \not \vdots p^2$ nên trong hai số $b_0$ và $c_0$ có đúng một số chia hết cho p, giả sử là $b_0$. Ngoài ra do $a_n=b_rc_s$ không chia hết cho $p$ nên $b_r$ không chia hết cho $p$. Suy ra, tồn tại k là số nhỏ nhất mà $0<k \le r \le n-k$ sao cho $b_k$ không chia hết cho p. Khi đó $b_0, b_1,..b_{k-1}$ đều chia hết cho $p$. Ta cũng có:
$a_k=b_kc_0+b_{k-1}c_1+..+b_0c_k$ là hệ số chia hết cho p. Tuy nhiên, do $b_kc_0 \not \vdots p$ và $b_0, b_1,..b_{k-1} \vdots p$ nên đây là điều mâu thuẫn. Vậy điều giả sử là sai và ta có đpcm.

Tiêu chuẩn mở rộng 2  (Tham khảo từ bài viết của STEVEN H. WEINTRAUB ): Cho $f(x)=a_nx^n+..+a_0$ là đa thức hệ số nguyên. Và giả sử có một số nguyên tố p sao cho $p$ không là ước $a_n$, $p$ là ước $a_i, (i=0,1,..n-1)$) và với một số số k nào đó $p^2$ không là ước của $a_k$. Gọi $k_0$ là giá trị nhỏ nhất của $k$ Khi đó nếu $f(x)=g(x)h(x)$ thì $min( deg g(x), deg h(x)) \le k_0$.

Chứng minh:
Gọi $deg g(x)=d_0$, $deg h(x)=e_0$. Gọi $d$ là số mũ nhỏ nhất của $x$ trong đa thức g(x) mà hệ số của nó không chia hết cho $p$, định nghĩa tương tự cho $e$. Khi đó:
$g(x)=x^dg_1(x)+pg_2(x)$,$h(x)=x^eh_1(x)+h_2(x)$. với các đa thức $g_1, g_2, h_1, h_2$ là các đa thức hệ số nguyên và các hệ số của $g_1, h_1$ không chia hết cho $p$. Khi đó:
$f(x)=g(x)h(x)=x^{d+e}g_1(x)h_1(x)+p(x^eh_1(x)g_2(x)+x^dh_2(x)g_1(x))+p^2g_2(x)h_2(x)$

mà theo giả thiết thì tất cả hệ số của $f(x)$ trừ $a_n$ đều chia hết cho $p$. Điều này dẫn đến $d+e=n$ vì nếu không ($x^{d+e}$ nhân với hệ số tự do trong $g_1(x)$ và $h_1(x)$ sẽ có được điều mâu thuẫn). và $ d \le d_0, e \le e_0$ $d_0+e_0=n$ nên $d=d_0, e=e_0$.

Vì thế $g(x)=b_{d_0}x^{d_0}+pg_2(x), h(x)=c_{e_0}x^{e_0}+ph_2(x)$ Trong trường hợp này ta có:

$f(x)=g(x)h(x)=a_nx^n+ph_2(x)b_{d_0}x^{d_0}+pg_2(x)c_{e_0}x^{e_0}+p^2g_2(x)h_2(x)$.

Vậy $k_0 \le min( deg g(x), deg h(x)) $ (điều phải chứng minh)
Lưu ý:
Với k=0 ta có tiêu chuẩn Eisentein f(x) bất khả quy còn $k=1$ nếu f(x) không có nghiệm hữu tỉ thì f(x) cũng bất khả quy.

Chứng minh một điểm là tâm đường tròn nội tiếp của tam giác

Bài toán: (Hải Phòng 2016) Cho tam giác nhọn ABC (AB<AC), phân giác trong đỉnh A cắt BC tại D, E là điểm trên đoạn BC sao cho BD=CE. Phân giác ngoài đỉnh A cắt đường thẳng qua D và vuông góc với BC tại F. I là trung điểm DF, đường thẳng EI cắt AD tại M, đường thẳng EF cắt đường thẳng qua M và vuông góc với BC tại K.
a) Đường thẳng AF cắt đường thẳng BC tại P, KD cắt đường tròn đường kính DF tại L (khác D). Chứng minh rằng đường thẳng PL tiếp xúc với đường tròn đường kính DF.
b) Chứng minh rằng I là tâm đường tròn nội tiếp tam giác KBC.

Lời giải:

a) Gọi N là giao điểm của KM và BC. Do I là trung điểm DF, DF// NK nên EI đi qua trung điểm NK. hay M là trung điểm NK
Ta có (LADF)=D(LADF)=D(KMNF)=-1 Vậy tứ giác ALFD điều hòa

Suy ra: tiếp tuyến tại L, AF, tiếp tuyến tại D đồng quy tại P hay PL là tiếp tuyến của đường tròn đường kính DF

b) Kẻ, BX, CY lần lượt là tiếp tuyến tới [DF]
(DXLY)=D(DXLY)=I(DBPC)=-1.Nên tứ giác DXLY điều hòa. Như vậy BX, CY, DL đồng quy

Gọi d là đường thẳng qua I song song BC, P là giao điểm EF và (I), M là trung điểm BC
Ta có:  (XYFP)=D(XYFP)=I(BCdM)=-1

Vậy tiếp tuyến tại X, Y, và FP cũng đồng quy.
Ta có đpcm

Nhận xét: Thực ra đây là bài toán ngược của bài toán: Cho tam giác ABC có (I) nội tiếp. (I) tiếp xúc với BC, CA, AB tại D, E, F. EF cắt BC tại P. AD cắt (I) tại L. Khi đó PL là tiếp tuyến thứ 2 của (I).

Dùng bậc và hệ số cao nhất trong bài toán đa thức.

Bài toán (Hà Nam 2016):

Cho $P,Q,R$ là $3$ đa thức hệ số thực thỏa mãn: $P(Q(x))+P(R(x))=c$ $\forall x\in\mathbb{R}$ với $c=const\in\mathbb{R}$

CMR: $P(x)\equiv const$ hoặc $[Q(x)+R(x)]\equiv const$


Lời giải:


Đặt $deg P(x)=p$ và không mất tính tổng quát giả sử $deg Q(x)=q \ge r=degR(x)$. Nếu $P(x)\equiv const$ hoặc $Q(x)\equiv const$ thì khi đó $R(x)\equiv const$ nên hai trường hợp này là hiển nhiên. Ta xét $ p,q >0$, $r \ge 0$

Đặt $C_k (f(x))$ là hệ số của $x^k$ trong đa thức $f(x)$, vì thế $C_{\deg f(x)} (f(x)) \neq 0$ là hệ số cao nhất của $f(x)$. Đặt $a = C_{\deg P(x)} (P(x))$, $b = C_{\deg Q(x)} (Q(x))$, $c = C_{\deg R(x)} (R(x))$.
Nếu $q>r$, Khi đó $C_{pq} (P(Q(x)) + P(R(x))) = ab^p \neq 0$, Vô lí. Vì thế ta phải có $q=r=m$, $\Rightarrow$ $C_{pm} (P(Q(x)) + P(R(x))) = a(b^p +c^p)\neq 0$, Theo điều kiện giả thiết thì $b^p + c^p = 0$, dẫn tới $p$ lẻ và $c=-b$.


Xét $a(Q(x)^p + R(x)^p) = a(Q(x)+R(x)) S(x)$, Trong đó $ S(x) = Q(x)^{p-1} - Q(x)^{p-2}R(x) + \cdots - Q(x)R(x)^{p-2} + R(x)^{p-1}$. Ta có $C_{(p-1)m}(S(x)) = b^{p-1} - b^{p-2}(-b) + \cdots - b(-b)^{p-2} + (-b)^{p-1} = pb^{p-1} \neq 0$, nên $\deg S(x) \geq (p-1)m$ (Thực ra là bằng luôn).


Mặt khác nếu đặt $T(x) = P(Q(x)) + P(R(x)) - a(Q(x)^p + R(x)^p)$ ta có $\deg T(x) \leq (p-1)m$. Giả sử ngược lại $Q(x)+R(x)$ không là hằng số, $\Rightarrow$ $\deg(Q(x)+R(x)) \geq 1$, Ta phải có $\deg(a(Q(x)^p + R(x)^p)) = \deg(a(Q(x)+R(x)) S(x)) \geq 1 + (p-1)m$, và vì thế $\deg(P(Q(x)) + P(R(x))) = \deg(a(Q(x)^p + R(x)^p) + T(x)) \geq 1+(p-1)m >0$, Mâu thuẫn.


Vậy ta có đpcm.
Ps: Nếu tồn tại $Q,R$ mà $Q(x) + R(x) = C$ là hằng số, ta vẫn có thể tìm đa thức $P$ khác hằng bậc$ p$ lẻ bất kì, để $P(Q(x)) + P(R(x)) $ là hằng số. Chỉ cần lấy $P(x) = (2x-C)^p + k/2$

Góc định hướng trong chứng minh hai đường tròn tiếp xúc.

Bài toán :

Cho $\triangle ABC$ nhọn nội tiếp $(O)$ với $I$ là tâm nội tiếp tam giác. Đường tròn đi qua $C$ tiếp xúc với $AI$ tại $I$ cắt $AC$ tại $E$ và cắt $(O)$ tại $H$ $(E,H\neq C)$

$a)$ CMR: $EH$ đi qua trung điểm của $AI$

$b)$ Đường tròn đi qua $B$ tiếp xúc với $AI$ tại $I$ cắt $AB$ tại $F$ và cắt $(O)$ tại $G$ $(G,F\neq B)$. CMR: $2$ đường tròn $(EIF)$ và $(GIH)$ tiếp xúc nhau

Lời giải:

a) Ta có (HA, HE)=(HA, HC)+(HC, HE)=(BA, BC)+(IC, IE)=(BA, BC)+(IC, IA)+(IA, IE)=(BA, BC)+(IC, IA)+(CI, CA)= (BA, AI) + (IA, IC)+(IC, BC)+ (CI, IA)+ (IC, CA) =(BA, AI)=(AI, AC) ( $\mod pi$ )

Như vậy MA là tiếp tuyến của (HEA).

Dùng phương tích $MA^2=MI^2=ME.MH$

b) Gọi IT là tiếp tuyến của (GIH) khi đó:
(IT, IE)=(IT, IH)+(IH, IE)=(IT, IH)+(CH, CA)=(GI, GH) +(BH, BA)= (GI, GF)+(GF, GH)+(BI, BF)= 2(BN, BA)+(GA, GH)+(GF, GA)= (BI, BF) +(BA, IA)
(FI, FE)= (FI, GF)+(GF, FE)= (BI, BG)+(HG, HE)=(BI, BA)+(BA, BG)+(HG, HA)+(HA, HE)= (BI, BA)+ (IA, AC)

Vậy IT cũng là tiếp tuyến tại I của (IEF) vậy ta có điều phải chứng minh.

Bài toán về tìm tất cả số k sao cho bất đẳng thức đúng.

Bài 1( Trường Hè 2016): Tìm tất cả các số thực $k$ sao cho tồn tại các số thực dương $a,b,c$ thỏa mãn $abc=1$ và $\frac{1}{{{a}^{k}}(b+c)}+\frac{1}{{{b}^{k}}(c+a)}+\frac{1}{{{c}^{k}}(a+b)}<\frac{3}{2}.$

Thực chất bài này tương đương với  Tìm tất cả các số thực $k$ sao cho với mọi số thực dương $a,b,c$ thỏa mãn $abc=1$ thì $\frac{1}{{{a}^{k}}(b+c)}+\frac{1}{{{b}^{k}}(c+a)}+\frac{1}{{{c}^{k}}(a+b)} \ge \frac{3}{2}.$

Lời giải:

- Xét trường hợp $k \ge 2$. Ta sẽ chứng minh $\frac{1}{{{a}^{k}}(b+c)}+\frac{1}{{{b}^{k}}(c+a)}+\frac{1}{{{c}^{k}}(a+b)} \ge \frac{3}{2}.$ với mọi $a,b,c$ dương thỏa mãn $abc=1$. Không mất tính tổng quát giả sử $ a \le b \le c$. Đặt: $x=\frac{1}{a}, y=\frac{1}{b},z=\frac{1}{c}$. Khi đó $x,y,z >0$ và $xyz=1$. Bất đẳng thức cần chứng minh trở thành:

$\sum \frac{x^{k-1}}{y+z} \ge \frac{3}{2}$

Ta có:$x \geq y\geq z \Rightarrow \frac{x}{y+z} \geq \frac{y}{z+x} \geq \frac{z}{x+y}$

Theo bất đẳng thức Chebyshev :

$(x^{k-2}+y^{k-2}+z^{k-2})(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}) \le 3(\frac{x^{k-1}}{y+z}+\frac{y^{k-1}}{z+x}+\frac{z^{k-1}}{x+y})$.

Mà theo Nesbitt: $\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y} \ge \frac{3}{2}$, và AM-GM: $x^{k-2}+y^{k-2}+z^{k-2} \ge 3$ nên:

$\frac{x^{k-1}}{y+z}+\frac{y^{k-1}}{z+x}+\frac{z^{k-1}}{x+y} \geq \frac{3}{2}$

Vậy $k \ge 2$ không thỏa mãn.

- Xét trường hợp $ \frac{1}{2}<k<2$ Cho $a=b=\frac{1}{n}$ $c=n^2$. Thì: 

$S=\frac{1}{{{a}^{k}}(b+c)}+\frac{1}{{{b}^{k}}(c+a)}+\frac{1}{{{c}^{k}}(a+b)}=\frac{2n^{k+1}}{n^3+1}+\frac{n^{1-2k}}{2}$

Khi đó $\underset{n \rightarrow  +\infty }{lim}S=0$, suy ra với $n$ đủ lớn thì $S  <\frac{3}{2}$ 

Vậy: $ \frac{1}{2}<k<2$ thỏa mãn.

- Xét trường hợp: $ \frac{1}{2}=k$. Cho $a=b=n$ $c=\frac{1}{n^2}$ Khi đó:

$S=\frac{2n^{2-\frac{1}{2}}}{n^3+1}+\frac{1}{2}$

Khi đó $\underset{n \rightarrow  +\infty }{lim}S=\frac{1}{2}$, suy ra với $n$ đủ lớn thì $S  <\frac{3}{2}$ 

Vậy $ \frac{1}{2}=k$ thỏa mãn.

- Xét trường hợp $-1 <k < \frac{1}{2}$. Chọn $a=b=n$ $c=\frac{1}{n^2}$ thì:

$S=\frac{2n^{2-k}}{n^3+1}+\frac{n^{2k-1}}{2} \Rightarrow \underset{n \rightarrow  +\infty }{lim}S=0$

Nên  $-1 <k < \frac{1}{2}$ thỏa mãn.

- Xét trường hợp $ k \le -1$. Ta chứng minh: $\frac{1}{{{a}^{k}}(b+c)}+\frac{1}{{{b}^{k}}(c+a)}+\frac{1}{{{c}^{k}}(a+b)} \ge \frac{3}{2}.$

Nếu đặt $h=1-k \ge 2$ thì theo chứng minh trên:

$\frac{1}{{{x}^{h}}(y+z)}+\frac{1}{{{y}^{h}}(z+x)}+\frac{1}{{{z}^{h}}(x+y)} \ge \frac{3}{2}\\\Leftrightarrow \frac{a^{h-1}}{b+c}+\frac{b^{h-1}}{c+a}+\frac{c^{h-1}}{a+b}  \geq \frac{3}{2} \\\Leftrightarrow \frac{a^{-k}}{b+c}+\frac{b^{-k}}{c+a}+\frac{c^{-k}}{a+b}  \geq \frac{3}{2} \\ \Leftrightarrow \frac{1}{{{a}^{k}}(b+c)}+\frac{1}{{{b}^{k}}(c+a)}+\frac{1}{{{c}^{k}}(a+b)} \ge \frac{3}{2}$

Vậy $ k \le -1$ không thỏa mãn điều kiện đề bài.

Kết luận: Tập giá trị $k$ cần tìm là: $\left ( -1;2 \right )$

Lưu ý $k=3$ là đề thi IMO 1995

Bài 2: (VN TST 2009) Tìm tất cả các số thực r sao cho bất đẳng thức:

$\prod \left ( r+\frac{a}{b+c} \right ) \ge (r+\frac{1}{2})^3$ Đúng với mọi a,b,c dương.

Lời giải:

Giả sử đúng với mọi bộ ba số thực dương a,b,c. Cho a=1, b=n, c=n, Khi đó:

$(r+\frac{1}{2n})(r+\frac{n}{n+1})^2 \ge(r+\frac{1}{2})^3$

Cho $n$ tiến đến vô cùng thì:

$r(r+1)^2 \ge (r+\frac{1}{2})^3 \Leftrightarrow r \in (-\infty ;\frac{-1-\sqrt{5}}{4}] \cup [\frac{-1+\sqrt{5}}{4};+\infty )$

Chuẩn hóa $a+b+c=1$, Khi đó bất đẳng thức đã cho tương đương:

$\prod \left ( \frac{r(b+c)+a}{b+c} \right ) \ge (r+\frac{1}{2})^3 \\\Leftrightarrow \prod (r+(1-r)a)\ge (r+\frac{1}{2})^3(1-a)(1-b)(1-c)\\\Leftrightarrow r^3+(1-r)^3abc+r(1-r)^2(ab+bc+ca)+r^2(1-r)(a+b+c) \ge (r+\frac{1}{2})^3(1-(a+b+c)+(ab+bc+ca)-abc)\\ \Leftrightarrow \left ( \sum ab \right )\left [ \left ( r+\frac{1}{2} \right )^3-r(1-r)^2 \right ] \le 8r^2+\left [ (1-r)^3+\left ( r+\frac{1}{2} \right )^3 \right ]abc\\ \Leftrightarrow \sum ab-\frac{9(4r^2-2r+1)}{28r^2-2r+1} abc \le \frac{8r^2}{28r^2-2r+1}$

Đặt $k=\frac{9(4r^2-2r+1)}{28r^2-2r+1}$ và $E=ab+bc+ca-kabc$. Với $r \in (-\infty ;\frac{-1-\sqrt{5}}{4}] \cup [\frac{-1+\sqrt{5}}{4};+\infty )$ thì $4r^2+2r-1 \ge 0$, suy ra $k \le \frac{9}{4}$

Ta chỉ cần chứng minh rằng: $E \le \frac{9-k}{27}=\frac{8r^2}{28r^2-2r+1}$ thì khi đó tập hợp các giá trị r cần tìm là $(-\infty ;\frac{-1-\sqrt{5}}{4}] \cup [\frac{-1+\sqrt{5}}{4};+\infty )$

Ta xét bài toán tổng quát hơn:

Cho số thực k. Xét các số thực không âm x,y,z thỏa mãn điều kiện x+y+z=1. Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức: E=xy+yz+zx-kxyz

Giải: Giả sử $ x \ge y \ge z$

Ta có: $\prod \left ( x+y-z \right ) \le xyz \Leftrightarrow \sum xy-\frac{9}{4}xyz \le \frac{1}{4}$

$xyz \le \frac{1}{27}$ (theo cô si cho 3 số)

Ta có:

$E=\sum xy-\frac{9}{4}xyz+(\frac{9}{4}-k)xyz$

Nếu $k <\frac{9}{4}$  thì:

$E \le \frac{1}{4}+\left ( \frac{9}{4}-k \right )\frac{1}{27}=\frac{1}{3}-\frac{k}{27}$

Nếu $k >\frac{9}{4}$ thì:

$E \le \sum xy-\frac{9}{4}xyz \le \frac{1}{4}$

nếu $k=\frac{9}{4}$ Thì $max E=\frac{1}{4}$

Tiếp theo tìm min E. Ta có $ x \ge \frac{1}{3}$

Nếu $k \le 0$ thì $E \ge 0$.

Nếu $ 0 < k < 9$ thì:

$E \ge 3 \sqrt[3]{(xyz)^2}-kxyz =\sqrt[3]{(xyz)^2}(3-k\sqrt[3]{xyz}) \ge \sqrt[3]{(xyz)^2}(3-\frac{k}{27}) \ge0$

Nếu $k =9$ thì:

$E=\sum xy-9xyz=yz(1-9x)+x(1-x) \ge \frac{(y+z)^2}{4}(1-9x)+x(1-x) =\frac{1-x}{4}(3x-1)^2 \ge 0$

Vậy min $E =0$

Khi $ k >9$ thì: 

$E=\sum xy-9xyz+(9-k)xyz \ge (9-k )xyz \ge \frac{9-k}{27}$

Lưu ý với $k=2$ là đề thi IMO 1984

Tính chất của số nguyên tố có dạng $3k+2$

Cho $p$ là số nguyên tố thỏa mãn $3 | p-2$ khi đó $p | x^3 -y^3$ khi và chỉ khi $p | x-y$

Chứng minh:

Ta xét $ x,y $ không chia hết cho $p$ vì nếu chia hết cho p là hiển nhiên.
Nếu $ x \equiv y (mod p)$ thì $ x^3 \equiv y^3 (mod p)$
Ta chứng minh Nếu $ x^3 \equiv y^3 (mod p)$ thì $ x \equiv y (mod p)$

$x^{3} \equiv y^3 (mod p)  \Rightarrow x^{p-2}\equiv y^{p-2}(mod p)$

Theo định lý Fermat nhỏ:

$x^{p-1}\equiv y^{p-1} \equiv 1(mod p) \Rightarrow x^{p-2}(x-y) \equiv 0 (mod p) \Rightarrow x \equiv y (mod p)$

Xét ứng dụng của bổ đề trên:

Bài toán ( Chọn đội tuyển QG tỉnh Lạng Sơn 2016): Cho đa thức $P(x)=4x^3-18x^2+27x+m$. CMR: Với mỗi $m\in\mathbb{Z}$, $\exists n\in\mathbb{Z}$ sao cho $P(n)\vdots 107$

Lời giải:
Do (2, 107)=1 nên:
$P(n)\vdots 107 \Leftrightarrow  2P(n)\vdots 107$

Xét $G(x)=2P(x)=(2x-3)^2+27+2m$

Với mỗi $m$ ta có $G(0), G(1), . G(106)$ lập thành một hệ thặng dư đầy đủ mod 107. Thật vậy:

Nếu có $i ,j $ mà $  0\ge i, j \le 106$ mà $G(i) \equiv G(j) (mod 107)$ Thì khi đó theo bổ đề trên:
 $i \equiv j (mod 107)$ hay $ i=j$.

Vậy luôn tồn tại $n$ sao cho $P(n)\vdots 107$

Một số tính chất số học của dãy tuyến tính

Cho dãy $(x_n)$ sao cho:
$x_0=1, x_1=1$, $x_{n+2}=ax_{n+1}+bx_n (a,b \in Z)$

Khi đó ta có:

1)$x_{m+n}=bx_{n}x_{m-1}+x_{n+1}x_{m}$

2) $x_{kn} \vdots x_n$

Ứng dụng:

Mở rộng đề thi chọn đội tuyển Ninh Bình 2016: Giả sử $p,q$ là hai số nguyên tố , dãy $(u_n)$ được xây dựng như sau:

$$\left\{\begin{matrix} u_0=0 & & & \\ u_1=1 & & & \\ u_n=pu_{n-1}-qu_{n-2}\forall n\geq 2,n \in \mathbb{N} & & & \end{matrix}\right.$$

Tìm tất cả $p,q$ biết tồn tại số tự nhiên $k$ để $u_{3k}=-3$

áp dụng tính chất 2) suy ra $u_3 |3 $ hay  $p^2-q|3$. Kết hợp điều kiện p,q nguyên tố nên có thể dễ dàng tìm được p,q

Dồn biến về biên để chứng minh bất đẳng thức

Bài toán:  $a,b,c$ là các số thực dương chứng minh:
            $ \frac{a}{4a+4b+c} + \frac{b}{4b+4c+a} + \frac{c}{4c+4a+b} \leq \frac{1}{3} $

Lời giải:

Ta nhân hai vế cho a+b+c rồi chuyển về bài toán sau:

 $a,b,c>0$.CM:$\frac{ab}{4b+4c+a}+\frac{bc}{4a+4c+b}+\frac{ac}{4b+4a+c}\leq \frac{a+b+c}{9}$

Trớ trêu thay bất đẳng thức này nếu xét a,b,c không âm thỏa mãn phân thức có nghĩa thì dấu bằng còn xảy ra khi a=0, b=2c !!

Không thể chứng minh $f(a,b,c) \ge f(a,t,t)$ được, ta sẽ dùng dồn biến về biên như sau:

Bdt tương đương
\[27(a^2b+b^2c+c^2a+abc) \leqslant 4(a+b+c)^3.\]
Đặt $f(a,\,b,\,c) = 27(a^2b+b^2c+c^2a+abc) - 4(a+b+c)^3,$ Ta chỉ ra rằng
\[f(a,\,b,\,c) \leqslant f(a+c,\,b,\,0) \leqslant 0.\]
Giả sử$b$ là số nằm giữa $c$ và $a,$ ta có
\[f(a,\,b,\,c)-f(a+c,\,b,\,0)=-27c(a-b)(b-c) \leqslant 0.\]
Vì thế
\[\begin{aligned} f(a,\,b,\,c) \leqslant f(a+c,\,b,\,0) & = 27b(c+a)^2-4(a+b+c)^3\\&=-(4a+b+4c)(a-2b+c)^2 \leqslant 0.\end{aligned}\]
Đẳng thức xảy ra khi và chỉ khi $(a,\,b,\,c) \sim (1,\,1,\,1)$ or $(a,\,b,\,c) \sim (0,\,1,\,2).$

Ngoài ra, một cách sử dụng bất đẳng thức Cauchy-Schwarz rất đẹp:

$\sum_{cyc}\frac{ac}{4a+4b+c}=\frac{1}{9}\sum_{cyc}\frac{ac(2+1)^2}{2(2a+b)+(2b+c)}\leq\frac{1}{9}\sum_{cyc}\left(\frac{2ac}{2a+b}+\frac{ac}{2b+c}\right)=\frac{a+b+c}{9}$

Dùng bất đẳng thức Muirhead để chứng minh bất đẳng thức

Bài toán: Chứng minh rằng với mọi $a,b,c$ không âm và $abc=1$ Thì
\[ \frac{1}{(1+a)^3}+\frac{1}{(1+b)^3}+\frac{1}{(1+c)^3}+\frac{5}{(1+a)(1+b)(1+c)} \ge 1  \]

Lời giải:

$\frac{1}{(1+a)^3}+\frac{1}{(1+b)^3}+\frac{1}{(1+c)^3}+\frac{5}{(1+a)(1+b)(1+c)} \ge 1\Leftrightarrow$
$\Leftrightarrow\sum_{cyc}(2a^2b^2+a^2b+a^2c+a^3-a^2-3a-1)\geq0\Leftrightarrow$
$\Leftrightarrow\sum_{cyc}(a^3-a^2)+2\cdot\sum_{cyc}(a^2b^2-a)+\frac{1}{2}\cdot\sum_{cyc}(a^2b+a^2c-2a)+$
$+\frac{1}{2}\cdot\sum_{cyc}(a^2b+a^2c-2)\geq0.$ Đúng theo Muirhead.

Ngoài ra $k_{max}=5,$
\[ \frac{1}{(1+a)^3}+\frac{1}{(1+b)^3}+\frac{1}{(1+c)^3}+\frac{k}{(1+a)(1+b)(1+c)} \ge \frac{k+3}{8}  \]