Bài toán : Cho các số nguyên dương  thỏa mãn hệ thức
thỏa mãn hệ thức  . Chứng minh rằng
. Chứng minh rằng 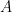 là lũy thừa bậc năm của một số nguyên.
là lũy thừa bậc năm của một số nguyên.
Lời giải :
Gọi 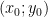 là cặp số thỏa mãn đề bài và có tổng
là cặp số thỏa mãn đề bài và có tổng 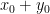 nhỏ nhất. Ta giả sử
nhỏ nhất. Ta giả sử  .
.
Xét phương trình bậc hai ẩn 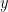 :
:
Vì 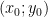 thỏa mãn đề bài nên
thỏa mãn đề bài nên  là một nghiệm của phương trình
là một nghiệm của phương trình  . Gọi nghiệm còn lại là
. Gọi nghiệm còn lại là 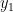 . Theo định lí
. Theo định lí  :
:
Ta có  nên từ
nên từ 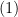 suy ra
suy ra  .
.
Các cặp  đều thỏa mãn
đều thỏa mãn  mà
mà 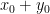 nhỏ nhất nên :
nhỏ nhất nên :
Như vậy 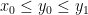
- Trường hợp 1 :
thay vào
thì
- Trường hợp 2 :
thì từ
ta được :
Dễ thấy  cùng tính chẵn lẻ mà
cùng tính chẵn lẻ mà 
Trường hợp này không xảy ra
- Trường hợp 3 :
Suy ra 
Do đó từ 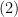 suy ra
suy ra 
Khi  thì từ
thì từ 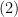 suy ra
suy ra  , vì
, vì  . Vô lí vì phải có
. Vô lí vì phải có  .
.
Tương tự khi xét  . Tất cả đều dẫn đến vô lí. Trường hợp này loại.
. Tất cả đều dẫn đến vô lí. Trường hợp này loại.
Do đó ta luôn có 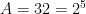 là lũy thừa bậc năm của một số nguyên. Đây là điều phải chứng minh.
là lũy thừa bậc năm của một số nguyên. Đây là điều phải chứng minh.
test code :) :)) =p~ =p~ cheer x-)
Trả lờiXóa