4 Cách chứng minh cho bài hình học APMO 2000

Bài toán: Cho  với trung tuyến  và phân giác . Đường thẳng vuông góc với  tại  cắt lần lượt tại . Đường thẳng vuông góc với  tại  cắt tại . Chứng minh: .

Lời giải 1.

---

Một cách tự nhiên ta nghĩ tới việc kéo dài  cắt 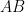 tại H.

Ta xét thêm PQ cắt  tại  ()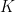

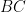Ta thấy:  là trung điểm của  mà  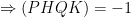 (Tính chất hàng điểm điều hòa)

 (Hệ thức Newton)

Mà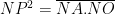 

Mà  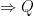 là trực tâm của 

 (đpcm).

Lời giải 2

Lời giải 3 (Khá giống lời giải 1 nhưng ý tưởng là chứng minh trùng và dùng cực, đối cực)

Giả sử đường thẳng qua O vuông góc BC cắt PR tại Q', Gọi E là giao điểm của đường thẳng qua A song song BC (đặt là l ) và PR.
Xét cực đối cực với (O)
Ta có Q thuộc đường đối cực của A nên A thuộc đường đối cực của Q nên l là đường đối cực của Q. (do l vuông góc OQ).

Từ đó do E là cực của AQ (Do đường đối cực của A là PR, đường đối cực của Q là l)

Gọi M' là giao AQ và BC. thì ta có:

 

Vậy M' là trung điểm BC. Suy ra Q trùng Q'. đpcm

Cách 4: Giả sử đường thẳng qua C và song song với AN cắt tia BA tại C'. 
Từ B kẻ đường vuông góc C'C cắt C'C tại T và tia AN tại U. 
Gọi A' là trung điểm CC'
Qua C kẻ đường thẳng song song với BT, đường này cắt bA ở V
Gọi chân đường thẳng vuông góc kẻ từ V xuống BT là W. Như thế CVWT là hình chữ nhật
AU là phân giác góc CAV và CV vuông góc với AU, nên U là trung điểm WT. 
Suy ra giao điểm N của AU và CW là tâm của hình chữ nhật CVWT, N chính là trung điểm CW. 
Ta đã có M là 
trung điểm BC. Vì M, N lần lượt là trung điểm các cạnh CB và CW của tam giác CBW nên
MN=BW/2
Do CC' song song AN ta có:
$\angle CC'A= \angle BAN= \angle CAN = \angle C'CA$
do đó AC'=AC.  Khi đó AU=C'T-C'A'. Mà N là tâm của hình chữ nhật CTWV nên $NU=\frac{1}{2}CT$ và

$AN=AU-NU=C'T-C'A'-\frac{1}{2}CT=\frac{1}{2}C'T$

Suy ra: $\frac{MN}{AN}=\frac{BW}{C'T}$ Nhưng MN song song với BW và NP nên:

$\frac{QN}{AN}=\frac{MN}{AN}=\frac{BW}{C'T}$

Bây giờ, ta có AN// VW và NP//BW, do đó các tam giác ANP và tam giác VWB đồng dang, và suy ra:

$\frac{AN}{NP}=\frac{VW}{BW}=\frac{CT}{BW}$

Từ đó ta được: $\frac{QN}{NP}=\frac{QN}{AN}.\frac{AN}{NP}=\frac{CT}{C'T}$

PN là đường cao của tam giác vuông ANO, nên hai tam giác ANP và PNO đồng dang. Từ đây ta suy ra:
$\frac{NP}{NO}=\frac{NA}{NP}$

Mặt khác, hai tam giác ANP và C'TB đồng dạng nên ta có:

$\frac{NA}{NP}=\frac{C'T}{BT}$

Do đó $\frac{QN}{NO}=\frac{QN}{NP}.\frac{NP}{NO}=\frac{CT}{C'T}.\frac{C'T}{BT}=\frac{CT}{BT}$

Ta lại có $\angle CTB$ và $\angle QNO$ là hai góc vuông nên hai tam giác $QNO$ và CTB đồng dạng, mà $NO 'perp BT$, do đó $QO \perp BC$