Có nhiều bài toán bất đẳng thức ở dạng tam giác lượng thì việc chứng minh rất dễ dàng . Xong khi nó bị mã hóa về dạng đại số thì sẽ khá gây khó dễ để chứng minh nếu ta không hình dung được bản chất lượng giác ban đầu của nó
1.1 Biểu diễn các đại lượng theo biến mới
Cho tam giác ABC có độ dài các cạnh là  .Đặt
.Đặt  ,
, 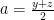 ,
, 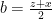 ,
,  hay
hay 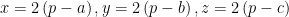 . Ta có các biểu diễn sau
. Ta có các biểu diễn sau
1.2 Xây dựng các bất đẳng thức đại số
Ví dụ 1. Cho các số thực  dương. Chứng minh rằng
dương. Chứng minh rằng 
HD: bất đẳng thức này được sinh ra từ bất đẳng thức 
Ví dụ 2. [Văn Đức Chín] Cho các số thực  dương có tổng bằng 1. Chứng minh rằng
dương có tổng bằng 1. Chứng minh rằng
HD: bất đẳng thức này được sinh ra từ bất đẳng thức 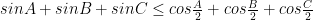
1.3. Bài tập
Bài 1. [Văn Đức Chín] Cho các số thực  dương . Chứng minh rằng
dương . Chứng minh rằng
Bài 2. [IMO,1983] Cho các số thực  dương . Chứng minh rằng
dương . Chứng minh rằng
Bài 3. [Văn Đức Chín] Cho các số thực  dương . Chứng minh rằng
dương . Chứng minh rằng
Bài 4. [Văn Đức Chín] Cho các số thực  dương . Chứng minh rằng
dương . Chứng minh rằng
Bài 5. [Văn Đức Chín]Cho các số thực  dương thỏa mãn
dương thỏa mãn 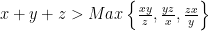 . Chứng minh rằng
. Chứng minh rằng 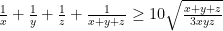
Bài 6. [MO Korea 1998] Cho các số thực  dương thỏa mãn
dương thỏa mãn 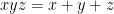 . Chứng minh rằng
. Chứng minh rằng
Bài 7. [Văn Đức Chín] Cho các số thực  dương , thỏa mãn
dương , thỏa mãn  . Chứng minh rằng
. Chứng minh rằng
Bài 8. [Văn Đức Chín] Cho các số thực  dương có tổng bằng 1 và thỏa mãn
dương có tổng bằng 1 và thỏa mãn 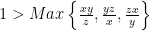 . Chứng minh rằng
. Chứng minh rằng
hay nhỉ
Trả lờiXóa