Chúng ta đã quen thuộc với việc sử dụng Tiêu chuẩn Schonemann -Eisenstein trong chứng minh đa thức bất khả qui. Ở bài viết này tôi sẽ trình bày thêm một số tiêu chuẩn khác có thể gọi là “sâu hơn” về tính bất khả qui của đa thức. Tuy nhiên để có một cách hệ thống tôi sẽ nhắc lại cả tiêu chuẩn Schonemann -Eisenstein ở đây.
Tiêu chuẩn 1.1. [Tiêu chuẩn Eisenstein] Cho  là đa thức với các hệ số nguyên và
là đa thức với các hệ số nguyên và 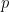 là số nguyên tố sao cho
là số nguyên tố sao cho  không chia hết cho
không chia hết cho 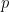 và các
và các  chia hết cho
chia hết cho 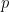 nhưng
nhưng 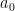 không chia hết cho
không chia hết cho  Khi đó
Khi đó 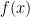 là đa thức bất khả qui trên
là đa thức bất khả qui trên 
Tiêu chuẩn 1.2. [Tiêu chuẩn Eisenstein suy rộng] Cho 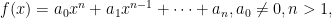 là đa thức với các hệ số nguyên và
là đa thức với các hệ số nguyên và 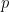 là số nguyên tố sao cho
là số nguyên tố sao cho 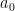 không chia hết cho
không chia hết cho 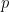 và các
và các  chia hết cho
chia hết cho 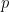 với
với  và
và  không chia hết cho
không chia hết cho  Nếu
Nếu 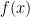 biểu diễn được thành tích của hai đa thức với hệ số nguyên,
biểu diễn được thành tích của hai đa thức với hệ số nguyên, 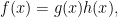 thì bậc của một trong hai đa thức
thì bậc của một trong hai đa thức 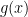 hoặc
hoặc 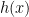 không nhỏ hơn
không nhỏ hơn 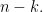
Ví dụ 1. Với bất kỳ số nguyên tố 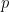 đa thức
đa thức  là bất khả quy trên
là bất khả quy trên 
Ví dụ 2. Với bất kỳ số nguyên dương  đa thức
đa thức 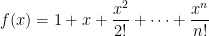 là bất khả quy trên
là bất khả quy trên 
Ví dụ 3. Cho 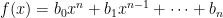 là đa thức với các hệ số nguyên và
là đa thức với các hệ số nguyên và 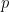 là số nguyên tố sao cho
là số nguyên tố sao cho 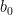 không chia hết cho
không chia hết cho 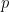 nhưng
nhưng  chia hết cho
chia hết cho 
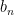 không chia hết cho
không chia hết cho  Khi đó
Khi đó 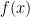 có nhân tử bất khả qui bậc
có nhân tử bất khả qui bậc 
Tiêu chuẩn 2.1. [Tiêu chuẩn Osada] Cho  là đa thức với các hệ số nguyên và
là đa thức với các hệ số nguyên và 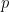 là số nguyên tố. Nếu
là số nguyên tố. Nếu  thì
thì 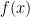 là bất khả qui.
là bất khả qui.
Chứng minh: Giả sử 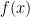 là khả qui. Khi đó
là khả qui. Khi đó 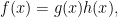 ở đó
ở đó 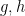 là những đa thức bậc dương với các hệ số nguyên. Vì
là những đa thức bậc dương với các hệ số nguyên. Vì 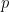 là số nguyên tố nên một trong các số hạng tự do của
là số nguyên tố nên một trong các số hạng tự do của  hay
hay 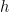 phải bằng
phải bằng 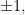 chẳng hạn hệ số tự do của
chẳng hạn hệ số tự do của  bằng
bằng  Vậy giá trị tuyệt đối của tích các nghiệm của
Vậy giá trị tuyệt đối của tích các nghiệm của  phải bằng 1. Khi đó
phải bằng 1. Khi đó 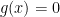 phải có một nghiệm
phải có một nghiệm 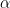 với
với  Vì
Vì 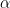 cũng là nghiệm của
cũng là nghiệm của  nên
nên  Điều mâu thuẫn này chứng tỏ
Điều mâu thuẫn này chứng tỏ 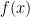 là bất khả qui.
là bất khả qui.
Tiêu chuẩn 2.2. [Tiêu chuẩn Osada mở rộng] Cho  là đa thức với các hệ số nguyên,
là đa thức với các hệ số nguyên, 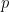 là số nguyên tố và
là số nguyên tố và 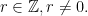 Nếu
Nếu 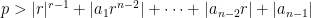 thì
thì 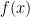 là bất khả qui trong
là bất khả qui trong ![\Bbb Z[x]. \Bbb Z[x].](https://s0.wp.com/latex.php?latex=%5CBbb+Z%5Bx%5D.&bg=ffffff&fg=000&s=0)
Ví dụ 4. Nếu  thì đa thức
thì đa thức  bất khả quy trong
bất khả quy trong ![\Bbb Z[x]. \Bbb Z[x].](https://s0.wp.com/latex.php?latex=%5CBbb+Z%5Bx%5D.&bg=ffffff&fg=000&s=0)
Ví dụ 5. Đa thức 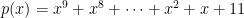 luôn luôn là bất khả quy.
luôn luôn là bất khả quy.
Tiêu chuẩn 3. [Tiêu chuẩn Polya] Cho 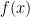 là đa thức bậc
là đa thức bậc  với các hệ số nguyên. Đặt
với các hệ số nguyên. Đặt ![m=[\dfrac{n+1}{2}]. m=[\dfrac{n+1}{2}].](https://s0.wp.com/latex.php?latex=m%3D%5B%5Cdfrac%7Bn%2B1%7D%7B2%7D%5D.&bg=ffffff&fg=000&s=0) Giả sử cho
Giả sử cho  số nguyên khác nhau
số nguyên khác nhau  có
có 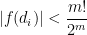 và các số
và các số  đều không là nghiệm của
đều không là nghiệm của  Khi đó
Khi đó 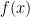 là bất khả qui
là bất khả qui
Chứng minh. Giả sử 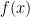 là một đa thức khả qui. Khi đó ta có biểu diễn
là một đa thức khả qui. Khi đó ta có biểu diễn 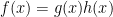 với
với 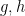 là những đa thức bậc dương, các hệ số nguyên. Hiển nhiên
là những đa thức bậc dương, các hệ số nguyên. Hiển nhiên  Không hạn chế ta có thể giả thiết
Không hạn chế ta có thể giả thiết  Ta có
Ta có  Ta thấy ngay
Ta thấy ngay  và
và  chia hết
chia hết 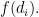 Do đó $
Do đó $ Khi đó có
Khi đó có 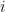 để
để 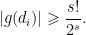 Vì
Vì 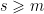 nên
nên 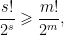 Thật vậy: hiển nhiên
Thật vậy: hiển nhiên  khi
khi 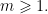 Vậy
Vậy 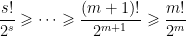 . Vậy
. Vậy 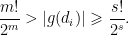 Mâu thuẫn này chỉ ra
Mâu thuẫn này chỉ ra 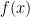 là một đa thức bất khả qui
là một đa thức bất khả qui
Ví dụ 6. [VMO 1984] Xác định đa thức bất khả quy ![f(x)\in \Bbb Z[x] f(x)\in \Bbb Z[x]](https://s0.wp.com/latex.php?latex=f%28x%29%5Cin+%5CBbb+Z%5Bx%5D&bg=ffffff&fg=000&s=0) nhận
nhận ![\sqrt{2}+\sqrt[3]{3} \sqrt{2}+\sqrt[3]{3}](https://s0.wp.com/latex.php?latex=%5Csqrt%7B2%7D%2B%5Csqrt%5B3%5D%7B3%7D&bg=ffffff&fg=000&s=0) làm một nghiệm.
làm một nghiệm.
Vid dụ 7. Với các số nguyên phân biệt  ký hiệu đa thức
ký hiệu đa thức  Nếu
Nếu 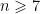 và
và ![ax^2+bx+1\in \Bbb Z[x],a\ne 0, ax^2+bx+1\in \Bbb Z[x],a\ne 0,](https://s0.wp.com/latex.php?latex=ax%5E2%2Bbx%2B1%5Cin+%5CBbb+Z%5Bx%5D%2Ca%5Cne+0%2C&bg=ffffff&fg=000&s=0) là bất khả quy thì
là bất khả quy thì 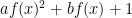 là bất khả quy.
là bất khả quy.
Ví dụ 8. Tìm tất cả các cặp 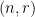 với số tự nhiên
với số tự nhiên  và số thực
và số thực  để đa thức
để đa thức  chia hết cho
chia hết cho 
Tiêu chuẩn 4. [Tiêu chuẩn Perron]} Giả sử ![f(x)=x^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0\in\Bbb Z[x] f(x)=x^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0\in\Bbb Z[x]](https://s0.wp.com/latex.php?latex=f%28x%29%3Dx%5En%2Ba_%7Bn-1%7Dx%5E%7Bn-1%7D%2B%5Ccdots%2Ba_1x%2Ba_0%5Cin%5CBbb+Z%5Bx%5D&bg=ffffff&fg=000&s=0) với bậc
với bậc  Nếu
Nếu 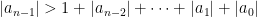 thì
thì 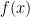 là đa thức bất khả quy trên
là đa thức bất khả quy trên
Chứng minh. Trước tiên ta chỉ ra 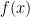 có đúng một nghiệm
có đúng một nghiệm 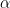 với môđun
với môđun  Giả sử
Giả sử  có nghiệm
có nghiệm  Khi đó
Khi đó 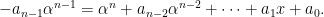 Nếu
Nếu  thì
thì 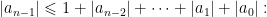 mâu thuẫn giả thiết. Do đó
mâu thuẫn giả thiết. Do đó  Giả sử
Giả sử  có các nghiệm phức
có các nghiệm phức  Ta có
Ta có 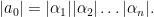 Vì
Vì 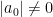 và nguyên nên
và nguyên nên  Vì
Vì  nên có
nên có 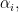 chẳng hạn:
chẳng hạn:  với
với 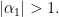 Đặt
Đặt 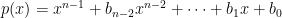 thỏa mãn
thỏa mãn  Khi đó ta có hệ
Khi đó ta có hệ  và có
và có  Do vậy
Do vậy  và suy ra
và suy ra 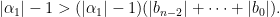 Vì
Vì  nên ta nhận được
nên ta nhận được  Với số phức
Với số phức  có
có 
Như vậy, mọi nghiệm  của
của  đều phải thỏa mãn
đều phải thỏa mãn 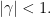 Tóm lại, ta đã chỉ ra
Tóm lại, ta đã chỉ ra 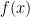 có đúng một nghiệm
có đúng một nghiệm 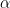 với môđun
với môđun  Giả sử
Giả sử 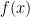 là khả quy với
là khả quy với 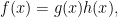 trong đó
trong đó ![g(x),h(x)\in \Bbb Z[x] g(x),h(x)\in \Bbb Z[x]](https://s0.wp.com/latex.php?latex=g%28x%29%2Ch%28x%29%5Cin+%5CBbb+Z%5Bx%5D&bg=ffffff&fg=000&s=0) và
và 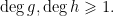 Vì
Vì 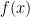 chỉ có một nghiệm với môđun lớn hơn 1 nên một trong hai đa thức, chẳng hạn
chỉ có một nghiệm với môđun lớn hơn 1 nên một trong hai đa thức, chẳng hạn 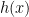 chỉ có các nghiệm với môđun nhỏ hơn 1. Giả sử
chỉ có các nghiệm với môđun nhỏ hơn 1. Giả sử 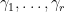 là tất cả các nghiệm của
là tất cả các nghiệm của  với
với  nguyên, khác 0. Ta có
nguyên, khác 0. Ta có  mâu thuẫn. Như vậy, điều giả sử là sai và suy ra
mâu thuẫn. Như vậy, điều giả sử là sai và suy ra 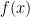 là đa thức bất khả quy.
là đa thức bất khả quy.
Tiêu chuẩn 5. [Tiêu chuẩn Brauer]} Giả sử đa thức ![f(x)=x^n-a_1x^{n-1}-\cdots-a_{n-1}x-a_n\in\Bbb Z[x] f(x)=x^n-a_1x^{n-1}-\cdots-a_{n-1}x-a_n\in\Bbb Z[x]](https://s0.wp.com/latex.php?latex=f%28x%29%3Dx%5En-a_1x%5E%7Bn-1%7D-%5Ccdots-a_%7Bn-1%7Dx-a_n%5Cin%5CBbb+Z%5Bx%5D&bg=ffffff&fg=000&s=0) với bậc
với bậc 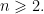 Nếu các hệ số
Nếu các hệ số  thì
thì 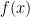 là đa thức bất khả quy trên
là đa thức bất khả quy trên 
Ví dụ 9. [IMO 1993]} Cho số tự nhiên 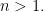 Chứng minh rằng, đa thức
Chứng minh rằng, đa thức 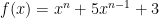 là bất khả quy trong
là bất khả quy trong ![\Bbb Z[x]. \Bbb Z[x].](https://s0.wp.com/latex.php?latex=%5CBbb+Z%5Bx%5D.&bg=ffffff&fg=000&s=0)
Ví dụ 10. Đa thức  bất khả quy trong
bất khả quy trong ![\Bbb Z[x]. \Bbb Z[x].](https://s0.wp.com/latex.php?latex=%5CBbb+Z%5Bx%5D.&bg=ffffff&fg=000&s=0)
………………………………Tiếp theo tôi sẽ viết bài tập …………………………..
Không có nhận xét nào:
Đăng nhận xét