Mộtt số kỹ thuật đổi biến
1.1 Điều kiện 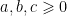 và
và 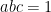
Trong trường hợp cần đổi biến thi có các cách đổi biến thường gặp sau
- Đổi biến
,
,
- Đổi biến
,
- Đổi biến
,
,
- Đổi biến
,
,
- Đổi biến
,
,
- Đổi biến
,
,
- Đổi biến
,
,
(Điều kiện các biến dương chỉ dùng khi cần thiết)
1.2. Điều kiện 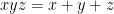
- Đổi biến
,
,
- Đổi biến
,
,
- Đổi biến
,
,
1.3. Điều kiện  . Đổi biến :
. Đổi biến : 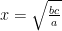 ,
,  ,
, 
1.4. Điều kiện 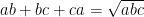 . Đổi biến :
. Đổi biến : 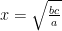 ,
,  ,
, 
1.5. Điều kiện 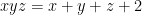 .
.
- Đổi biến
,
- Đổi biến
,
,
,
1.6. Điều kiện 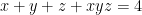
- Đổi biến
,
,
- Đổi biến
,
,
,
,
1.7. Điều kiện  Đổi biến
Đổi biến  ,
,  ,
, 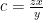 . Khi đó ta sẽ có
. Khi đó ta sẽ có 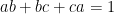
1.8. Điều kiện  Đổi biến
Đổi biến  ,
, 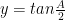 ,
, 
1.9. Điều kiện 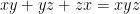 Đổi biến
Đổi biến  ,
,  ,
, 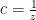
1.10. Điều kiện 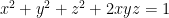 Đổi biến x=cosA, y=cosB, z=cosC
Đổi biến x=cosA, y=cosB, z=cosC
Bài tập áp dụng
Bài 1. Cho  là các số thực dương thỏa mãn
là các số thực dương thỏa mãn 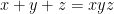 . Chứng minh rằng
. Chứng minh rằng
Lời giải 1 . (Dùng đổi biến)
Đặt  ,
, 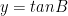 ,
, 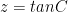 . Từ giả thiết ta có A,B,C là 3 góc của một tam giác và yêu cầu bài toán trở thành: chứng minh rằng
. Từ giả thiết ta có A,B,C là 3 góc của một tam giác và yêu cầu bài toán trở thành: chứng minh rằng  . Đây là một bất đẳng thức cơ bản trong tam giác có nhiều cách chứng minh. Chẳng hạn theo bđt Jensen
. Đây là một bất đẳng thức cơ bản trong tam giác có nhiều cách chứng minh. Chẳng hạn theo bđt Jensen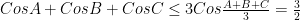
Lời giải 2. (Dùng AM_GM)
Nhận xét: Lời giả 1 dễ dàng hơn trong suy luận, Lời giải 2 cần sự tinh tế hơn trong biến đổi
Bài 2. Cho các số thực dương 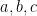 có
có  . Chứng minh rằng
. Chứng minh rằng 
Lời giải. Đặt 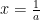 ,
, 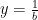 ,
,  . Áp dụng AM-GM
. Áp dụng AM-GM 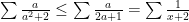 . Ta cần chứng minh
. Ta cần chứng minh  . Điều này hiển nhiên vì
. Điều này hiển nhiên vì 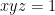
Bài 3. Cho các số thực 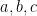 có
có  . Chứng minh rằng
. Chứng minh rằng 
Lời giải. Đặt 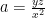 ,
, 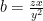 ,
, 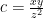 . Bất đẳng thức đã cho trở thành cần chứng minh
. Bất đẳng thức đã cho trở thành cần chứng minh 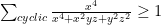 . Áp dụng bđt CBS ta có
. Áp dụng bđt CBS ta có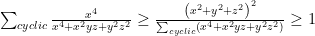 . Điều này hiển nhiên vì bđt cuối cùng tương đương với
. Điều này hiển nhiên vì bđt cuối cùng tương đương với 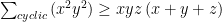
Bài 4. Cho các số thực dương  thỏa mãn điều kiện
thỏa mãn điều kiện 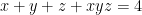 . Tìm hằng số k tốt nhất sao cho
. Tìm hằng số k tốt nhất sao cho 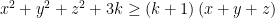
ĐS 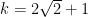
Bài 5. Cho các số thực dương  thỏa mãn điều kiện
thỏa mãn điều kiện 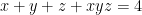 .Chứng minh rằng
.Chứng minh rằng 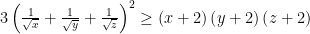
Bài 6. Cho các số thực dương  thỏa mãn điều kiện
thỏa mãn điều kiện 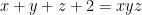 .Chứng minh rằng
.Chứng minh rằng
Bài 7. Cho các số thực dương  thỏa mãn điều kiện
thỏa mãn điều kiện 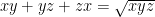 .Chứng minh rằng
.Chứng minh rằng 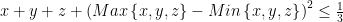
Bài 8. Cho các số thực dương  thỏa mãn điều kiện
thỏa mãn điều kiện  . Chứng minh rằng
. Chứng minh rằng 
2. Các kết quả quen thuộc từ một điều kiện
2.1 Điều kiện 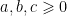 và
và 
Giả thiết này ta liên hệ đến một số kết quả quen thuộc sau
- Trong một số trường hợp khác có thể đổi biến : a=x+1,b=y+1, c=z+1
Bạn đọc tự chứng minh một số kết quả trên
ngon cảm ơn nhé :))
Trả lờiXóa