Một bổ đề hai đường tiếp xúc và ứng dụng

Ta có bổ đề sau: Cho tam giác ABC, trên BC lấy hai điểm D, E sao cho AD, AE đẳng giac trong góc A khi và chỉ khi (ADE) tiếp xúc (ABC).

Bổ đề được chứng minh bằng cách kẻ tiếp tuyến tại A của (ABC) rồi sau đó cộng góc đơn giản có thể suy ra tiếp tuyến tại A của (ABC) cũng là tiếp tuyến tại A của (ADE) suy ra đpcm.

Bài toán 1 (Brazil 2011):  Cho tứ giác ABCD nội tiếp (O), r và s là hai tiếp tuyến tại B, C của (O). r, s cắt AD tại M và N. BN cắt CM tại E. AE cắt BC tại F và L là trung điểm BC. Chứng minh (DLF) tiếp xúc (O).

Gọi K là giao điểm của r và s. Ta có L là trung điểm của BC và cần chứng minh (DFL) tiếp xúc (DBC) là (O), mà L là trung điểm BC. nên ta chỉ cần chứng minh DF là đối trung của tam giác DBC hay D,F,K thẳng hàng.

Áp dụng định lí Sin và Menelaus ta có:

$\frac{sin\angle BKF}{sin\angle FKC}=\frac{BF}{FC}=\frac{BE}{EC}\frac{sin\angle AEN}{sin\angle MEA}=\frac{BE}{EC}\frac{AN}{AM}\frac{ME}{EN}=\frac{ME}{EC}\frac{BE}{EN}\frac{AN}{AM}=\frac{MB}{BK}\frac{NK}{NC}\frac{MB}{MK}\frac{CK}{CN}\frac{AN}{AM}=\frac{MB^{2}}{NC^{2}}\frac{NK}{MA}\frac{NA}{MK}=\frac{MD}{MK}\frac{NK}{ND}=\frac{sin\angle MKD}{sin\angle DKN}$

Từ đây siu ra F, D, K thẳng hàng ta có đpcm
cách 2:
Gọi $ X=BM \cap CN, Y=AD \cap BC, Z=AC \cap BD $ .

Vì $ BC $ là đường đối cực của $ X $ đối với $ (O) $ ,
từ $ X(E,Y;C,B)=-1 $ ta có $ XE $ là đường đối cực của $ Y $ đối với $ (O) $ .
vì $ XZ $ là đường đối cực $ Y $ đối với $ (O) $ ,
nên $ X, E, Z $ thẳng hàng và $ C(B,A;N,M)=B(C,D;M,N) $ ,
vì thế $ (Y,F;B,C)=(Y,A;N,M)=C(B,A;N,M)=B(C,D;M,N)=(Y,D;M,N) $ .
suy ra $ D, F, X $ thẳng hàng

Vì $ DF $ là đường đối trung $ \triangle DBC $ ,
ta nhận đc $ \angle BDL=\angle FDC $ and $ (DLF) $ tiếp xúc $ (O) $ tại $ D $ .

Bài toán 2 : Cho tam giác $ABC$ nội tiếp $(O)$. $M,N$ trên $(O)$ sao cho $MN\parallel BC$ và $AB$ nằm giữa $AM,AC$. $CM$ cắt $BN$ tại $S$. $BM$ cắt $CN$ tại $T$. $P$ là một điểm trên $(O)$. $PT$ cắt đường thẳng qua $S$ song song $BC$ tại $Q$. Chứng minh rằng $(QPS)$ tiếp xúc với $(O)$

Lời giải

Gọi $ T'=PT \cap \odot (O) $ và $ S'=PS \cap \odot (O) $ .
Đặt $ \{ X, Y \}=SQ \cap \odot (O) $ và $ \{ U, V \}=TS \cap \odot (O) $ .

Vì $ SQ $ là đường đối cực của $ T $ đối với $ \odot(O) $ ,
nên $ P(T', S'; U, V)=(T, S; U, V)=-1 $ ,
kết hợp với $ \angle UPV=90^{\circ} $ suy ra $ \angle BPQ=\angle SPC $ . ... $ ( \star ) $
vì $ \angle XPB=\angle CPY $ ( $ \because XY \parallel BC $ ) ,
kết hợp với $ (\star) $ ta có $ \angle XPQ=\angle SPY $ ,
vì thế theo bổ đề trên $ \odot (PQS) $ tiếp xúc $ \odot (O) $ tại $ P $ .

Dùng phép nghịch đảo để đơn giản hóa bài toán

Bài toán: Cho tam giác $ABC$ nội tiếp $(O)$. $P$ là một điểm nằm trong tam giác và nằm trên phân giác trong của $\angle BAC$. Gọi $E,F$ là điểm chính giữa của cung $AC,AB$. $AE$ giao đường tròn $(APC)$ tại điểm thứ hai là $M$, $AF$ giao đường tròn $(APB)$ tại điểm thứ hai là $N$. Chứng minh rằng: $MN\parallel EF$

Lời giải:

Xét phép nghịch đảo tâm $A$ phương tích bất kì, ta đưa bài toán đã cho về bổ đề sau:

Bổ đề. Cho $\Delta ABC,P$ là điểm bất kì trong tam giác và thuộc phân giác trong góc $A.E,F$ là các điểm trên tia đối $CB,BC$ sao cho $CE=CA,BF=BA.$

Gọi $M,N=AE,AF \cap CP,BP.$ Khi đó $(AEF)$ tiếp xúc $(AMN).$

Hay EF song song MN như vậy ta đã làm mất hết các đường tròn và đưa về bài toán THCS.

Gọi I và I' lần lượt là tâm nội tiếp và chân đường phân giác trong góc A.

Theo định lí Menelaus, $\frac{MA}{ME}.\frac{EC}{CI'}.\frac{I'P}{PA}=1=\frac{NA}{NF}.\frac{FB}{BI'}.\frac{I'P}{PA}.$

Theo định lí Thales, $\frac{EC}{CI'}=\frac{AI}{II'}=\frac{FB}{BI'} \Rightarrow \frac{MA}{ME}=\frac{NA}{NF} \Rightarrow MN \parallel EF \Rightarrow (AEF)$ tiếp xúc $(AMN)$ (đpcm).

Góc định hướng trong chứng minh hai đường tròn tiếp xúc.

Bài toán :

Cho $\triangle ABC$ nhọn nội tiếp $(O)$ với $I$ là tâm nội tiếp tam giác. Đường tròn đi qua $C$ tiếp xúc với $AI$ tại $I$ cắt $AC$ tại $E$ và cắt $(O)$ tại $H$ $(E,H\neq C)$

$a)$ CMR: $EH$ đi qua trung điểm của $AI$

$b)$ Đường tròn đi qua $B$ tiếp xúc với $AI$ tại $I$ cắt $AB$ tại $F$ và cắt $(O)$ tại $G$ $(G,F\neq B)$. CMR: $2$ đường tròn $(EIF)$ và $(GIH)$ tiếp xúc nhau

Lời giải:

a) Ta có (HA, HE)=(HA, HC)+(HC, HE)=(BA, BC)+(IC, IE)=(BA, BC)+(IC, IA)+(IA, IE)=(BA, BC)+(IC, IA)+(CI, CA)= (BA, AI) + (IA, IC)+(IC, BC)+ (CI, IA)+ (IC, CA) =(BA, AI)=(AI, AC) ( $\mod pi$ )

Như vậy MA là tiếp tuyến của (HEA).

Dùng phương tích $MA^2=MI^2=ME.MH$

b) Gọi IT là tiếp tuyến của (GIH) khi đó:
(IT, IE)=(IT, IH)+(IH, IE)=(IT, IH)+(CH, CA)=(GI, GH) +(BH, BA)= (GI, GF)+(GF, GH)+(BI, BF)= 2(BN, BA)+(GA, GH)+(GF, GA)= (BI, BF) +(BA, IA)
(FI, FE)= (FI, GF)+(GF, FE)= (BI, BG)+(HG, HE)=(BI, BA)+(BA, BG)+(HG, HA)+(HA, HE)= (BI, BA)+ (IA, AC)

Vậy IT cũng là tiếp tuyến tại I của (IEF) vậy ta có điều phải chứng minh.

IMO shortlist 2002 và những vấn đề liên quan.

Đề bài: Đường tròn nội tiếp (I) của tam giác ABC tiếp xúc với BC tại K. Gọi M là trung điểm đường cao AD. KM cắt (I) tại N. Chứng minh rằng (BCN) tiếp xúc với (I) tại N.

Lời giải:

Đặt $S=KA\cap \Omega$,và đặt $T$ là điểm đối xứng $K$ qua I . Gọi $X,Y$ là các tiếp điểm của (I) trên $CA,AB$.

$AD$ // $KT$ nên $(KT,KN;KS,KD)=-1$. suy ra $KTSN$ điều hòa, vậy tiếp tuyến với $(I)$ tại $K,S$ đồng quy trêb $NT$. Mặt khác, tiếp tuyến tại $X,Y$ đồng quy $KS$, nên $KXSY$ là tứ giác điều hòa, Nghĩa là tiếp tuyến tại $K,S$ đồng quy $XY$.

Từ đây suy ra $BC,XY,TN$ Đồng quy. Gọi $P=XY\cap BC$, suy ra $(B,C;K,P)=-1$,và vì $\angle KNP=\angle KNT=\frac{\pi}2$, nên $NK$ là phân giác của $\angle BNC$.

Gọi $B'=NB\cap \Omega,\ C'=NC\cap \Omega$, Ta có:
$BB^{\prime} \cdot BN = BK^2$
$CC^{\prime} \cdot CN = CK^2$. Suy ra:
$\frac{BB^{\prime} \cdot BN}{CC^{\prime} \cdot CN} = \frac{BK^2}{CK^2}$
Nhưng NK là phân giác của góc BNC nên:
$\frac{BK}{CK} = \frac{BN}{CN}$
Vì vậy:
$\frac{BB^{\prime} \cdot BN}{CC^{\prime} \cdot CN} = \frac{BN^2}{CN^2}$
Suy ra:
$\frac{BB^{\prime}}{CC^{\prime}} = \frac{BN}{CN}$
Nên:
 $B'C'\|BC$, nên $N$ là tâm vị tự biến $(I)$ thành $(BNC)$ Hay (I) tiếp xúc (BNC) tại N vậy ta có điều phải chứng minh.

Ta có thêm những kết quả sau:

-NK đi qua tâm bàng tiếp góc A. (Gọi M là trung điểm BC và lưu ý AT đi qua tiếp điểm bàng tiếp trên BC Dùng hàng điểm để chứng minh)

-Nếu gọi $N_B$ tương tự như điểm N ứng với góc B, $N_C$ ứng với góc C thì $NK, N_BX, N_CY$ đồng quy tại S thuộc OI( Dùng cực đối cực)

-  Trục đẳng phương của $N_BAC, N_CAB$ và $N_BX, N_CY$ đồng quy tại một điểm thuộc OI. ( ý đầu dùng định lý 4 điểm, ý sau có thể dùng tâm vị tự, cực đối cực) suy ra điểm đồng quy này là S.

Ngoài ra rất nhiều bài toán đẹp có thể được phát triển từ những mô hình này.

Từ bổ đề đường tròn tiếp xúc đến bài toán mở rộng Serbia 2016

$\boxed{\text{Bài toán}}$(Serbia 2016) Cho tam giác $ABC$ có đường cao $AH$ và tâm nội tiếp $I$. $IB,IC$ cắt $AH$ tại $M,N$. $K,L$ là tâm ngoại tiếp tam giác $MAB,NAC$. $R,Q$ là trung điểm $IB,IC$. Lấy $P$ sao cho $PR\perp NL,PQ\perp MK$. Một tiếp tuyến thay đổi của đường tròn Euler của tam giác $IBC$ cắt $PQ,PR$ tại $S,T$. $X$ đối xứng $P$ qua $S,T$. Chứng minh rằng đường tròn $(XST)$ luôn tiếp xúc một đường tròn cố định khi tiếp tuyến thay đổi.

Lời giải:

Ta cần có hai bổ đề sau:

$\boxed{\text{Bổ đề 1}}$ Cho tam giác $ABC$ có $O$ là tâm ngoại tiếp. Một đường tiếp tuyến với $\odot (BOC)$ cắt $AB$ ở $D$ và $CA$ ở $E$. Gọi $A'$ là điểm đối xứng của điểm $A$ qua $DE$. Khi đó $\odot (A'DE)$ tiếp xúc $\odot (ABC)$.

Chứng minh. Gọi $X$ là tiếp điểm $BX,CX$ cắt $\odot (O)$ tại $K,L.KE,LD$ cắt nhau tại $S$. Theo định lí $Pascal$ đảo thì $S$ thuộc $\odot (O)$


Biến đổi góc: $\angle DSE=\angle LCK=\angle BXC-\angle BKC=\angle BOC-\angle BAC=\angle BAC=\angle DA'E$

$\Longrightarrow D,S,A',E$ đồng viên.

Mặt khác: $\angle EXC=\angle KBC=\angle ESC$ nên $E,L,S,C$ đồng viên.

$\Longrightarrow E,X,S,C$ đồng viên.

$\Longrightarrow \angle DES=\angle XCS=\angle LKS$

$\Longrightarrow DE\parallel KL$

$\Longrightarrow \odot (DSE)$ tiếp xúc $\odot (DLK)$ hay $\odot (A'DE)$ tiếp xúc $\odot (ABC).\blacksquare$

$\boxed{\text{Bổ đề 2}}$ Cho tam giác $IBC.Q,R$ lần lượt là trung điểm $IC,IB$. Kí hiệu $\omega $ là đường tròn $Euler$ của $\triangle IBC.PR,PQ$ cắt $\omega $ tại $F,E$. Khi đó tâm $\odot (PEF)$ thuộc $\omega $.

Chứng minh. Gọi $I'$ là trung điểm $BC$.



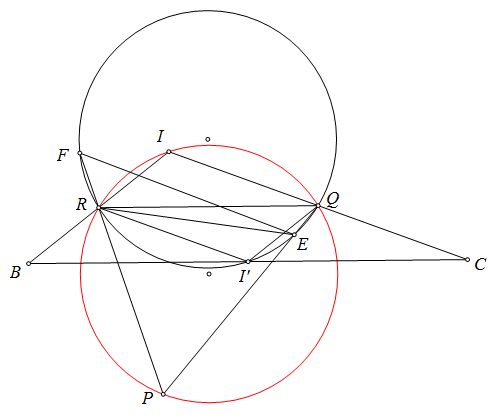
Ta có $\angle RPE=180^\circ-\angle RIQ=180^\circ-\angle RI'Q=180^\circ-\angle REQ=\angle REP$

$\Longrightarrow \angle FRE=2\angle FPE\Longrightarrow $ tâm $\odot (PEF)$ thuộc $\omega .\blacksquare$

Quay lại bài toán.

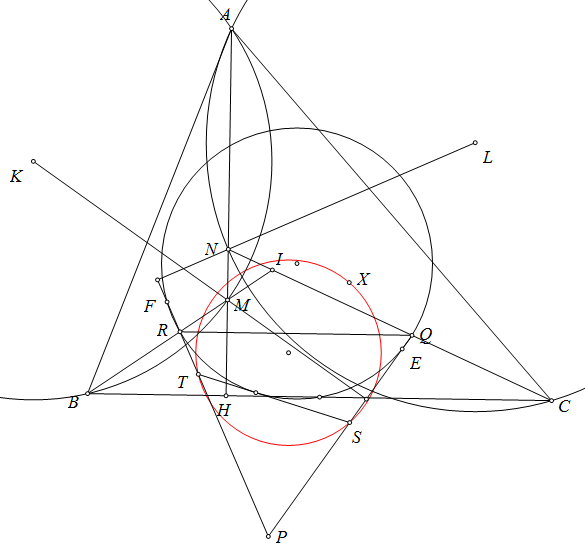
Ta có $\angle IQP=90^\circ-\angle IMN+\angle AMK=90^\circ-\angle B/2+\angle C/2$. Tương tự $\angle IRP=90^\circ-\angle C/2+\angle B/2$.

Gọi $E,F$ lần lượt là giao của $PQ,PR$ với đường tròn $Euler$ của tam giác $IBC$. Theo bổ đề $2$ ta suy ra tâm $\odot (PEF)$ thuộc đường tròn $Euler$ của tam giác $IBC$. Theo bổ đề $1$ ta suy ra $\odot (PEF)$ tiếp xúc $\odot (XST).\blacksquare$