Một số bài toán về đường tròn Mixtilinear

Bài 1: Cho tam giác ABC nội tiếp (O), đường tròn Mixtilinear  trong góc A tiếp xúc (O) tại P. Phân giác góc A cắt BC và (O) tại Q, M. đường tròn bàng tiếp góc A tiếp xúc BC tại N. Chứng minh rằng MN và PQ cắt nhau trên (O).

Lời giải:

Xét phép f: nghịch đảo tâm A phương tích AB.AC và phép đối xứng qua phân giác góc A, ta có:
f biến B thành C, C thành B, biến Q thành M.
qua phép nghịch đảo điểm P' là điểm tiếp xúc của đường tròn bàng tiếp góc A của tam giác AB'C' nên qua phép đối xứng phân giác P chính là N.

Do phép đối xứng phân giác ta có $\angle PAQ=  \angle NAM$
Mặt khác AP.AN=AB.AC=AQ.AM suy ra tam giác APQ và tam giác AMN đồng dạng suy ra A là tâm của phép vị tự quay biến PQ thành MN, suy ra PQ và MN cắt nhau trên (O).

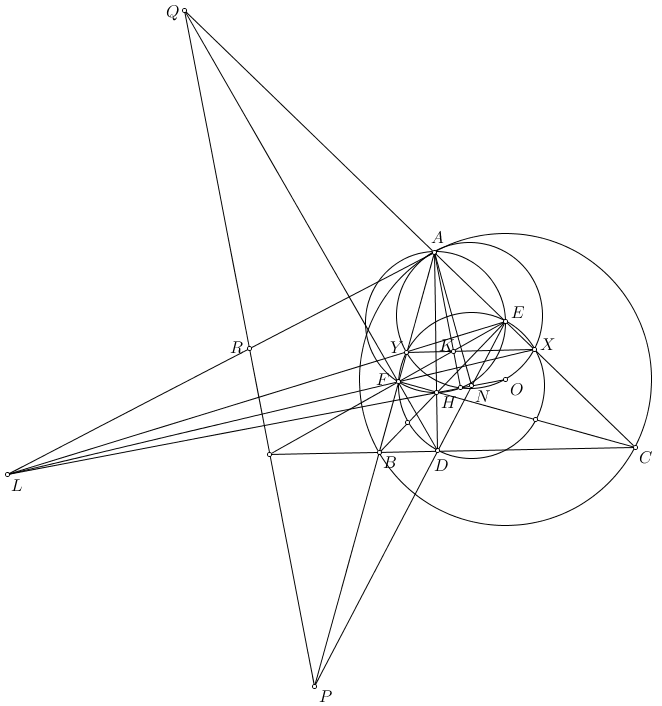
Bài 2: Cho $\triangle ABC$ Gọi $I_A$ và $I$ là đường tròn bàng tiếp góc A and tâm đường tròn nội tiếp. Gọi $A$-mixtilinear (gọi là $\Gamma$), và $(I_A)$ tiếp xúc $(ABC)$ và $BC$ tại $T$ và $D$, theo thứ tự đó. Gọi $AI\cap (ABC)=\{ M\}$ và $(TMI)\cap \Gamma=\{ E\}\neq T$.
$\textbf{a.)}$ CMR $I_ADEI$ nội tiếp.
$\textbf{b.)}$ Giả sử $(I_ADI)\cap \Gamma=\{ S\}\neq E$, CMR khi đó $(BSC)$ tiếp xúc$\Gamma$.

Lời giải:

Ta sẽ vẽ hình câu a) và b) riêng để cho dễ nhìn:

a)

Phép nghịch đảo đối xứng qua phân giác góc A phương tích AB.AC biến E là giao của (w) và (IMT) thành E' là giao cả $(I_A)$ và $(DLI_A)$. Mặt khác Do góc LD$I_A$ vuông tại D và DL là tiếp tuyến của $(I_A)$từ đây suy ra $E'L$ cũng là tiếp tuyến của $(I_A)$ suy ra LE'=LD $\Rightarrow AE'=AD$ như vậy AB.AC=AE'.AE=AD.AE=AI.$AI_A$ suy ra điều phải chứng minh.

b)  

Gọi $\Phi$ là phép nghịch đảo tâm $A$ phương tích $\sqrt{AB\cdot AC}$ và đối xứng qua phân giác $\angle BAC$. Gọi $ID\cap (I_A)=R$, $MD\cap (ABC)=\{ G \}$, $\Gamma \cap AB,\ AC=\{ X\},\ \{Y\}$, $XY\cap BC=\{ Z\}$, gọi $A_H$ là chân đường cao từ $A$ và $A_1$ là điểm đối xứng của $A$ qua tâm $(ABC)$.

Ta chứng minh hai bổ đề:

Bổ đề 1: MD, TK, $I_AA_1$ đồng quy.

Chứng minh: Theo bài 1 thì MD và TK đồng quy trên (O) ta gọi điểm đó là G

Dễ thấy $AKDG$ nội tiếp (do phương tích), vì thế $\angle ZDA=\angle KDA=\angle KGA=\angle TMA=\angle ZMA$, nên $ZMDA$ nội tiếp, $$\Phi(MD)\cap \Phi(KT)\in \Phi((ABC))=BC\Longrightarrow \Phi(G)=Z\ . \ . \ . \ \spadesuit$$

để ý rằng  $\angle AIZ=90^{\circ}=\angle AA_HZ\Longrightarrow AIA_HZ$ nội tiếp, nhưng vì, $AA_1$($A_1\in (ABC)$) và $AA_H$($A_H\in BC$)$\Longrightarrow A_1=\Phi( A_H),\ I_A=\Phi(I),\ G\stackrel{\spadesuit}{=}\Phi(Z)$ thẳng hàng.

Bổ đề 2; Cho tam giác ABC có I là tâm nội tiếp, D là tiếp điểm bàng tiếp góc A trên BC, ID cắt đường tròn bàng tiếp góc A tại S. CMR (BSC) tiếp xúc đường tròn bàng tiếp góc A

Gọi tâm của đường tròn bàng tiếp góc A $A$ và $(BCS)$ là $E,O$. Gọi $DS$ là giao điểm của $(BCS)$ và SD tại $X$. Theo bài toán quen thuộc hai đường tròn này tiếp xúc nhau $\iff$ $XO\parallel DE$ $\iff$ $OX\perp BC$ $\iff$ $DS$ chia đôi $\angle BSC$.

Gọi $G$ là chân đường vuông góc từ $I$ tới $BC$. $F$ trên $BC$ sao cho $(B,C;D,F)=-1$. theo hàng điểm điều hòa $DS$ phân giác $\angle BSC$ $\iff$ $\angle FSD=90$ $\iff$ $I,G,S,F$ Đồng viên

Gọi $M$ là trung điểm $BC$, nên cũng là trung điểm $GD$(Dễ chứng minh). Gọi $N$ là trung điểm của $DS$, nếu $I,G,S,F$ đồng viên $\iff$ $I,M,N,F$ đồng viên (dùng đường đối song) $\iff$ $MD.DF=ID.DN$. Vì $N$ là trung điểm $DS$, suy ra $EN\perp IS$, có nghĩa là $I,B,E,N,C$ đồng viên $\Rightarrow$ $ID.DN=BD.DC$. Dùng tính chất hàng điểm điều hòa $MD.DF=BD.DC$. Vì thế $ID.DN=BD.DC=MD.DF$, Điều phải chứng minh.

Vào bài toán:

Chú ý bổ đề [b]bổ đề 1[/b] nên $MD$, $KT$ và $I_AA_1$ đồng quy trên $(ABC)$.

Vì $$\angle I_AIZ=90^{\circ}=I_ADZ\Longrightarrow Z\in (I_ADI)\ . \ . \ . \ \bigstar$$

Và $$\Phi(D)=T\stackrel{\bigstar}{\Longrightarrow} \Phi((I_ADIZ))\stackrel{\spadesuit}{=}(GTII_A)=\omega\ . \ . \ . \ \clubsuit$$.

Nếu $N$ là trung điểm $AA_H$, theo bổ đề quen thuộc $R$, $I$, $D$ và $N$ thẳng hàng.$\blacksquare$

Nếu ta chứng minh $R\in \omega$, Khi đó dùng bổ đề 2, ta có điều phải chứng minh.

$\begin{align*}R\in \omega\Longleftrightarrow \angle I_ARI&= \angle I_AGI\\&= \angle A_1GI\\
&= \angle A_1GK+\angle KGI\\&\stackrel{\text{Bo de}}{=} \angle A_1GT+\angle TGI\\&\stackrel{\clubsuit}{=} \angle A_1AT +\angle TI_AI\\&\stackrel{AD\text{ va } AT,\ AA_1\text{ va } AA_H \text{dang giac}}{=} \angle A_HAD+\angle TI_AA\\&= \angle A_HAD+\angle A\Phi(T)\Phi(I_A)=\angle A_HAD+\angle ADI\\&\stackrel{\blacksquare}{=} \angle NAD+\angle ADN\\&= \angle DNA_H\\&\stackrel{I_AD||NA_H}{=}\angle RDI_A\\&\stackrel{I_AD=I_AR=\text{ban kinh }(I_A)}{=}\angle I_ARD\\&= \angle I_ARI
\end{align*}.$

Bài 3: Cho $\triangle ABC$ có tâm nội tiếp $I$, tâm bàng tiếp với góc $A$, $I_A$, nội tiếp $\Gamma$. Gọi giao điểm của đường tròn Mixtilinear ngoài và trong góc A tiếp xúc $\Gamma$ tại $P$ và $Q$, theo thứ tự đó, $AI\cap BC=\{ K \}$ và $AI\cap \Gamma=\{ L \}$ đường tròn nội tiếp $\triangle ABC$ tiếp xúc $BC$ tại $D$. $A_1$ là điểm đối xứng của $A$ qua tâm $\Gamma$ và $QL\cap BC=\{ T \}$, Chứng minh $\odot (KDA)$, $\odot (I_API)$, $A_1I$, $AT$, $PK$ và $LD$ đồng quy trên $\Gamma$.

1:AT,LD đồng quy trên $\odot ABC$ 

Chiếu $(A,C;B,Q)$ từ $L$ đến $\odot ABC$($AT\cap \odot ABC={R}$)

$$L(A,Q;B,C)=(K,T;B,C)=A(K,T;B,C)=(L,R;B,C)=\frac{LB\cdot RC}{RB\cdot LC}=\frac{RC}{RB}=\frac{AB\cdot QC}{QB\cdot AC}$$

Nghịch đảo $\mathcal{I}_{L,LC}$ : $BC$ $\rightarrow$ $\odot ABC$vì thế ( $BD\cap \odot ABC={R'}$):

$$\frac{BD}{BR'}=\frac{BL\cdot LD}{BL^2}=\frac{CD}{CR'}$$

Do $AQ$ đẳng giác với AZ ($Z$ tiếp điểm đường tròn bàng tiếp trên BC)

$$\frac{AB\cdot QC}{QB\cdot AC}=\frac{BZ}{CZ}=\frac{BD}{CD}=\frac{RC}{RB}=\frac{R'C}{R'B}$$

Vì $Z,D$ đẳng giác vì thế $R\equiv R'$.$\clubsuit$

2:$\odot KDA$ qua $R$

Xét phép nghịc đảo $\mathcal {I} _{L,LB}$ biến $BC$ thành $\odot ABC$ và $D$ $\rightarrow$ $R$,$K$ $\rightarrow$ $A$

Ta có $LD\cdot LR=LK\cdot LA=LB^2$ Vì thế $KDAR$ nội tiếp.$\clubsuit$

3:$PK$ qua $R$

Xét phép nghịch đảo cực A phương tích AB.AC và đối xứng qua phân giác $\angle BAC$ ta có đường tròn Mixtilinear ngoại thành đường tròn nội tiếp và $AQ$ thành $AD$ vì thế $AQ$ đẳng giác với nhau trong góc $A$..Đặt $RK\cap \odot ABC={P'}$:

$$\angle ALP'=\angle KDR =\angle KAD$$

Suy ra $AP',AD$ đẳng giác nên ta có đpcm.$\clubsuit$

4:$\odot PII_{A}$ qua $T$

$P,K,R$ thẳng hàng $BK\cdot KC=PK\cdot KR=IK\cdot KI_{A}$ và $\odot PII_{A}R$ nội tiếp.$\clubsuit$

5 :$A_{1}I$ qua $R$

Phép nghịch đảo $\mathcal {I}_{L,LB}$ cố định $\odot IDR$ và $IL$ là tiếp tuyến của nó.Gọi $IR\cap \odot ABC={A'_{1}}$, $F$ là chân đường cao từ $A$ đến $BC$:

$$\angle A'_{1}AL=\angle LRI=\angle LID=\angle KAF=\angle A_{1}AL$$

Vì thế $A_{1}\equiv A'_{1}$ đpcm.$\clubsuit$.

Bài 4 (APMC 2016): Cho $\triangle ABC$ có đường tròn Mixtilinear trong góc A , $\omega$, Và tâm bàng tiếp $I_A$. Gọi $H$ là chân đường cao từ $A$ đến $BC$, $E$ trung điểm cung $\overarc{BAC}$ và $M$,$N$, là trung điểm $BC$ ,$AH$, theo thứ tự đó. Giả sử $MN\cap AE=\{ P \}$ Và $I_AP$ cắt $\omega$ tại $S$ và $T$ theo thứ tự: $I_A-T-S-P$. CMR: đường tròn ngoại tiếp $\triangle BSC$ và $\omega$ tiếp xúc nhau.

Lời giải:

Ta đặt lại $ S $ là điểm mà $ \odot (BSC) $ tiếp xúc $ \omega $ tại $ S $ và $ P $ là giao điểm $ AE, $ $ MN. $ Ta sẽ cm rằng $ I_A, $ $ P, $ $ S $ thẳng hàng. Gọi $ I $ là tâm nội tiếp của $ \triangle ABC $ và đặt $ J $ $ \in $ $ IN $ là điểm tiếp xúc của $ \odot (I_A) $ với $ BC. $ Đặt $ V $ $ \in $ $ EI $ là điểm tiếp xúc của $ \omega $với đường tròn ngoại tiếp $ \triangle ABC $ , $ D $ là giao điểm của $ BC, $ $ EI. $ Vì $$ \frac{I_AA}{I_AI} = \frac{JN}{JI} = \frac{1}{2} \cdot \frac{\text{dist}(A,BC)}{\text{d}(E,BC)} \cdot \frac{\text{d}(E,BC)}{\text{d}(I,BC)} = \frac{PA}{PE} \cdot \frac{DE}{DI} \ , $$Dùng định lý Menelaus cho $ \triangle AIE $ và $ D, $ $ P, $ $ I_A $ we get $ I_A, $ $ D, $ $ P $ thẳng hàng $ \qquad $ $ (\ddagger). $

Mặt khác cực của $ X $ thuộc $ SV $ đối với $ \omega $ nằm trên $ BC, $ chú ý đường tròn tâm $ X $ bán kính $ XD $ $ = $ $ XS $ $ = $ $ XV $ là đường tròn Appolonius của góc V của $ \triangle BVC $ ta được $ SD $ phân giác $ \angle BSC $ Do bài 2b) thì $DII_A$ đi qua điểm S, mặt khác tứ giác $I_AID'J$ nội tiếp (D' là giao của đường thẳng qua I vuông góc AI), từ đây suy ra $SI_A \perp SD'$ mặt khác SD vuông SD' do phân giác và phân giác ngoài $ \Longrightarrow $ $ I_A, $ $ D, $ $ S $ thẳng hàng (, kết hợp với $ (\ddagger) $ kết luân $ I_A, $ $ D, $ $ P, $ $ S $ thẳng hàng.

Bài 5: (Đề thi HSGS lớp 10, vòng 2):

Tam giác $ABC$ nội tiếp đường tròn $(O)$, đường tròn $(K)$ tiếp xúc $(O)$ tại $D$ và tiếp xúc $AC,AB$ lần lượt tại $E,F$. $AL$ là đường kính của $(O)$. $KE,KF$ lần lượt cắt $LB,LC$ tại $M,N$.Chứng minh rằng $AD\perp MN$

Lời giải:

Gọi $ T $ là giao điểm thứ hai của $ \odot (O) $ với đường tròn đường kính $ AK $ và gọi $ J $ $ \equiv $ $ AT $ $ \cap $ $ EF. $ Rõ ràng, $ J $ là tâm đẳng phương$ \odot (K), $ $ \odot (O), $ $ \odot (AK), $ vì thế$ DJ $tiếp xúc $ \odot (K) $ và$ \odot (O) $ tại $ D. $ Mặt khác, $ TA, $ $ TK $ phân giác$ \angle ETF, $ cắt tại $ X $ thuộc $ EF, $ $ TK $ liên hợp $ J $ đối với $ E, $ $ F, $ Vì thế$ A, $ $ D, $ $ X $ nằm trên cực của $ J $ đối với $ \odot (K). $ Vì $ KMLN $ là hình bình hành$ KL $ đi qua trung điểm $ MN, $ Kết luân $$   (\perp MN, AT; AE, AF) = (\perp MN, \perp LK; \perp LC, \perp LB) = -1 = A( X, T; E, F) \Longrightarrow AD \perp MN. $$

Cách khác nghịch đảo: Xem tại đây

Hai bài 6,7 lấy từ anh Quang Dương
Bài toán 6: Cho $\triangle ABC$, đường tròn mixtilinear nội tiếp và bàng tiếp góc $\widehat{BAC}$ của $\triangle ABC$ là $(I_a)$ và $(J_a)$ tiếp xúc $(ABC)$ thứ tự tại $P, Q$. $PQ$ cắt $BC$ tại $E$. Khi đó $AE$ tiếp xúc $(BAC)$.



Chứng minh:
Xét phép nghịch đảo cực $A$ phương tích $AB.AC$ hợp với phép đối xứng trục phân giác góc $\widehat{BAC}$:
$I_{A}^{AB.AC} \circ Đ_{l} : X \Leftrightarrow X' $.
Khi đó $C \equiv B', B \equiv C'$. $P', Q'$ thứ tự là tiếp điểm của đường tròn bàng tiếp góc $A$ và nội tiếp của $\triangle ABC$ với đường thẳng $BC$. Khi đó $P', Q'$ đối xứng nhau qua trung trực $BC$. Qua $A$ kẻ đường thẳng song song với $BC$ cắt $(ABC)$ tại điểm thứ hai $R$ thì $R \in (AP'Q')$. Do đó $R \equiv E'$. $AR, AE$ đẳng giác nên $AE$ là tiếp tuyến của $(ABC)$.
Bài toán 7: Cho tam giác $ABC$ nội tiếp $(O)$. Đường tròn mixtilinear nội tiếp góc $A$ là $(I_a)$ của $\triangle ABC$ tiếp xúc $AB, AC$ và $(O)$ tại $D, E, F$. $AF$ cắt $DE$ tại $L$. Đường thẳng qua $L$ vuông góc $OA$ cắt $BC$ tại $G$. Khi đó $FG$ tiếp xúc $(O)$.



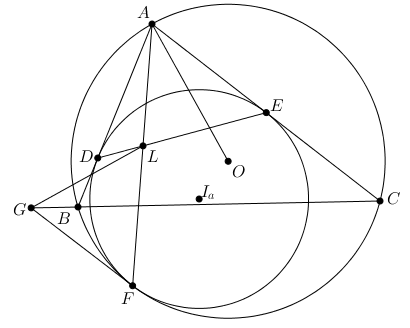
Chứng minh:
$DE$ cắt $BC$ tại $K$. Gọi $I$ là tâm nội tiếp $\triangle ABC$. $AH$ là đường cao tam giác $ABC$. Ta có $(LG, LK) \equiv (AO, AI_a) \equiv (AI, AH) \equiv (KL, KG)$ (mod $\pi$). Do đó $\triangle GLK$ cân tại $G$. Hơn nữa ta có tính chất: $AI$ cắt $FK$ tại $J$ là điểm chính giữa cung $BC$ không chứa $A$ của tam giác $ABC$. Ta có $(FK, FA) \equiv (FJ, FA) \equiv (BJ, BA) \equiv (BJ, BC) + (BC, BA) \equiv (AJ, AC ) + \frac{\pi}{2} - (OA, AC) \equiv (AJ, AO) + \frac{\pi}{2} \equiv \frac{\pi}{2} - (LG, LK)$ (mod $\pi$). Do đó $G$ là tâm $(DKF)$. Suy ra $(FG, FA) \equiv \frac{\pi}{2} - (DE, FJ) \equiv \frac{\pi}{2} - (DE, AJ) + (JF, JA) \equiv (CF, CA)$. Do vậy $GF$ là tiếp tuyến của $(O)$.

Bài 8 (Mạnh Tuấn): Cho $\triangle ABC$, đường tròn Mixtilinear nội tiếp xúc $(O)$ tại $D$, tiếp xúc $CA,AB$ tại $E,F$. Tiếp tuyến tại $D$ của $(O)$ cắt $BC$ tại $P$.$AD$ cắt $EF$ tại $L$. Khi đó $PL \perp AO$
Chứng minh Gọi $f(X)$ là ảnh của $X$ qua phép nghịch đảo $I^A_{AB.AC}$ hợp với phép đối xứng trục qua phân giác $\angle BAC$
Khi đó $f(B)= C, f(C) = B, f((I)) = (J)$ là đường tròn bàng tiếp $\angle A$. $f(D), f(E), f(F) $ là tiếp điểm của $(J)$ với $BC,CA,AB$. $f(L) $ là giao của $Af(D)$ với$ (Af(E)f(F))$. $f(P)$ là giao của đường tròn qua $D$ tiếp xúc $BC$ và $(ABC)$


Viết lại bài toán dưới cấu hình đường tròn nội tiếp, ta được bài toán tương đương :
Cho $\triangle ABC$ với đường tròn nội tiếp $(I)$ tiếp xúc $BC,CA,AB$ tại $D,E,F$. $AH$ là đường cao ($H \in BC$). $AD$ cắt $(AEF)$ tại $M$. Đường tròn qua $A,M$ trực giao với $AH$ cắt $(O)$ tại $G$. Chứng minh rằng $(AGD)$ tiếp xúc $(O)$


$IM$ cắt $BC$ tại $S$. Khi đó $S,E,F$ thẳng hàng.
Gọi $A'$ đối xứng $A$ qua $O$, $IM$ cắt $AH$ tại $R$ và $T$ là trung điểm $ID$
Theo 1 bài toán quen thuộc thì $R,T,A'$ thẳng hàng. Lại có $\angle AGR = 90^{\circ}$ nên $G,R,T,A'$ thẳng hàng
$X$ là trung điểm $SD$ , $AX$ cắt $(O)$ tại $G'$, $G'A'$ cắt $ID$ tại $T'$
Ta có $XD^2 = XB.XC = XG'.XA \implies (AG'D)$ tiếp xúc $(I)$ tại $D$
Gọi $K$ là tâm $(AG'D)$ .Khi đó $K,I,D$ thẳng hàng
Có $\angle XG'D = \angle XT'D = 90^{\circ} - \angle KDA \implies SH \perp AD$
Lại có $SI \perp AD \implies T'X \parallel IS \implies T'$ là trung điểm $ID$
Vậy $G \equiv G' \implies (AGD)$ tiếp xúc $BC$. Ta có điều cần chứng minh

Một bổ đề hai đường tiếp xúc và ứng dụng

Ta có bổ đề sau: Cho tam giác ABC, trên BC lấy hai điểm D, E sao cho AD, AE đẳng giac trong góc A khi và chỉ khi (ADE) tiếp xúc (ABC).

Bổ đề được chứng minh bằng cách kẻ tiếp tuyến tại A của (ABC) rồi sau đó cộng góc đơn giản có thể suy ra tiếp tuyến tại A của (ABC) cũng là tiếp tuyến tại A của (ADE) suy ra đpcm.

Bài toán 1 (Brazil 2011):  Cho tứ giác ABCD nội tiếp (O), r và s là hai tiếp tuyến tại B, C của (O). r, s cắt AD tại M và N. BN cắt CM tại E. AE cắt BC tại F và L là trung điểm BC. Chứng minh (DLF) tiếp xúc (O).

Gọi K là giao điểm của r và s. Ta có L là trung điểm của BC và cần chứng minh (DFL) tiếp xúc (DBC) là (O), mà L là trung điểm BC. nên ta chỉ cần chứng minh DF là đối trung của tam giác DBC hay D,F,K thẳng hàng.

Áp dụng định lí Sin và Menelaus ta có:

$\frac{sin\angle BKF}{sin\angle FKC}=\frac{BF}{FC}=\frac{BE}{EC}\frac{sin\angle AEN}{sin\angle MEA}=\frac{BE}{EC}\frac{AN}{AM}\frac{ME}{EN}=\frac{ME}{EC}\frac{BE}{EN}\frac{AN}{AM}=\frac{MB}{BK}\frac{NK}{NC}\frac{MB}{MK}\frac{CK}{CN}\frac{AN}{AM}=\frac{MB^{2}}{NC^{2}}\frac{NK}{MA}\frac{NA}{MK}=\frac{MD}{MK}\frac{NK}{ND}=\frac{sin\angle MKD}{sin\angle DKN}$

Từ đây siu ra F, D, K thẳng hàng ta có đpcm
cách 2:
Gọi $ X=BM \cap CN, Y=AD \cap BC, Z=AC \cap BD $ .

Vì $ BC $ là đường đối cực của $ X $ đối với $ (O) $ ,
từ $ X(E,Y;C,B)=-1 $ ta có $ XE $ là đường đối cực của $ Y $ đối với $ (O) $ .
vì $ XZ $ là đường đối cực $ Y $ đối với $ (O) $ ,
nên $ X, E, Z $ thẳng hàng và $ C(B,A;N,M)=B(C,D;M,N) $ ,
vì thế $ (Y,F;B,C)=(Y,A;N,M)=C(B,A;N,M)=B(C,D;M,N)=(Y,D;M,N) $ .
suy ra $ D, F, X $ thẳng hàng

Vì $ DF $ là đường đối trung $ \triangle DBC $ ,
ta nhận đc $ \angle BDL=\angle FDC $ and $ (DLF) $ tiếp xúc $ (O) $ tại $ D $ .

Bài toán 2 : Cho tam giác $ABC$ nội tiếp $(O)$. $M,N$ trên $(O)$ sao cho $MN\parallel BC$ và $AB$ nằm giữa $AM,AC$. $CM$ cắt $BN$ tại $S$. $BM$ cắt $CN$ tại $T$. $P$ là một điểm trên $(O)$. $PT$ cắt đường thẳng qua $S$ song song $BC$ tại $Q$. Chứng minh rằng $(QPS)$ tiếp xúc với $(O)$

Lời giải

Gọi $ T'=PT \cap \odot (O) $ và $ S'=PS \cap \odot (O) $ .
Đặt $ \{ X, Y \}=SQ \cap \odot (O) $ và $ \{ U, V \}=TS \cap \odot (O) $ .

Vì $ SQ $ là đường đối cực của $ T $ đối với $ \odot(O) $ ,
nên $ P(T', S'; U, V)=(T, S; U, V)=-1 $ ,
kết hợp với $ \angle UPV=90^{\circ} $ suy ra $ \angle BPQ=\angle SPC $ . ... $ ( \star ) $
vì $ \angle XPB=\angle CPY $ ( $ \because XY \parallel BC $ ) ,
kết hợp với $ (\star) $ ta có $ \angle XPQ=\angle SPY $ ,
vì thế theo bổ đề trên $ \odot (PQS) $ tiếp xúc $ \odot (O) $ tại $ P $ .

Dùng hàng điểm điều hòa để chứng minh đồng quy

Đề bài:

Cho tam giác ABC không đều trực tâm H, tâm đường tròn ngoại tiếp O,đường cao AD. Gọi E là giao điểm của OA với BC. 1 đường thẳng $\Delta$ đi qua D và song song với đường thẳng Euler của tam giác cắt AB,AC lần lượt tại M,N. I là trung điểm của AE. DI cắt AB ,AC lần lượt tại P,Q.Chứng minh rằng MQ,NP,OD đồng quy biết MQ cắt NP tại T.

Lời giải:

Gọi BB', CC' là 2 đường cao của tam giác ABC. B'C' cắt AD tại J. Ta có (A, H, J, D) = -1.

Gọi K là giao điểm của MN và AO
AO cắt (O) tại điểm thứ 2 là G. Ta có tam giác AB'C' đồng dạng tam giác ABC nên phép vị tự quay tâm A biến J thành H, E thành G. Dễ dàng suy ra JE//HG

Vậy ta có hệ thức $\frac{AJ}{AH}=\frac{AE}{AG}=\frac{AI}{AO}$

Hay JI song song với HO, hay JI song song với DK.

Do đó (A, O, I, K) = -1.

Vậy D(A, O, I, K) = -1, từ đó có MQ, NP, OD đồng quy ( bằng cách gọi giao điểm của OD và AB, AC).

Phép nghịch đảo để chứng minh thẳng hàng

Bài toán: Gọi $ H,O$ là trực tâm và tâm ngoại tiếp $ \Delta ABC$. Đường tròn ngoại tiếp và đường tròn Euler của $ \Delta HBC$ cắt nhau tại $ \{M,N \}$. Gọi $ O^*$ là tâm đường tròn ngoại tiếp $ \Delta AMN$ và $ L$ là trung điểm của $ OA$. Chứng minh rằng $ H,O^*,L$ thẳng hàng            

Lời giải:

Gọi    $ A’,B’,C’$ là chân đường cao đến các cạnh $ BC,CA,AB.$ $ F$ là trung điểm $ BC$  Gọi $ B’C’$ cắt $ BC$ tại $ P$ và cắt $ (O)$ tại $ B’',C’'.$ Vì $ (B,C,A’,P) =- 1,$ nên  $ PB \cdot PC = PA’ \cdot PF$ $ \Longrightarrow$ $ PB’' \cdot PC’' = PA’ \cdot PF$ $ \Longrightarrow$ $ F \in \odot(A’B’'C’').$ Vì thế tâm của $ \odot(A’B’'C’')$ là đường thẳng qua vuông góc từ $ A$ đến $ B’C’$ giao với trung trực $ A’F,$ chính là trung điểm $ L$ của $ AO.$ Phép nghịch đảo $ \mathcal{I}$ tâm $ H,$ biến $ (O)$ thành đường tròn chín điểm $ \mathcal{N},$ và biến $ B’C’$ thành đường tròn ngoại tiếp $ \triangle HBC$ và $ \odot(A’B’'C’')$ thành đường tròn đi qua $ A$ và Giao điểm $M,N$ của $ \mathcal{N}$ và $ \odot(HBC),$ Là ảnh của $ A’,C’',B’'$ $ \Longrightarrow$ phép nghịch đảo tâm $ H,$ biến tâm ngoại tiếp $ L$ của $\odot (A’B’'C’')$ và tâm $ O^*$ của tam giác $ \odot(AMN)$ thẳng hàng.

Dùng hàng điểm điều hòa để chứng minh vuông góc.

Bài toán: Cho tam giác ABC, đường cao BE, CD. gọi F, G là hình chiếu của D, E trên BC. DG cắt EF tại M. Chứng minh rằng AM vuông BC.

Lời giải:

Gọi P, Q là hình chiếu của A, M trên BC.
$U \equiv MQ \cap DE,$  $V \equiv AP  \cap DE$ và $L \equiv DE \cap BC.$

Vì $EG \parallel DF,$ theo bổ đề hình thang  $M(D,E,U,L)=-1,$ nhưng $(D,E,V,L)=-1$ vậy ta có đpcm

Chứng minh một điểm là tâm đường tròn nội tiếp của tam giác

Bài toán: (Hải Phòng 2016) Cho tam giác nhọn ABC (AB<AC), phân giác trong đỉnh A cắt BC tại D, E là điểm trên đoạn BC sao cho BD=CE. Phân giác ngoài đỉnh A cắt đường thẳng qua D và vuông góc với BC tại F. I là trung điểm DF, đường thẳng EI cắt AD tại M, đường thẳng EF cắt đường thẳng qua M và vuông góc với BC tại K.
a) Đường thẳng AF cắt đường thẳng BC tại P, KD cắt đường tròn đường kính DF tại L (khác D). Chứng minh rằng đường thẳng PL tiếp xúc với đường tròn đường kính DF.
b) Chứng minh rằng I là tâm đường tròn nội tiếp tam giác KBC.

Lời giải:

a) Gọi N là giao điểm của KM và BC. Do I là trung điểm DF, DF// NK nên EI đi qua trung điểm NK. hay M là trung điểm NK
Ta có (LADF)=D(LADF)=D(KMNF)=-1 Vậy tứ giác ALFD điều hòa

Suy ra: tiếp tuyến tại L, AF, tiếp tuyến tại D đồng quy tại P hay PL là tiếp tuyến của đường tròn đường kính DF

b) Kẻ, BX, CY lần lượt là tiếp tuyến tới [DF]
(DXLY)=D(DXLY)=I(DBPC)=-1.Nên tứ giác DXLY điều hòa. Như vậy BX, CY, DL đồng quy

Gọi d là đường thẳng qua I song song BC, P là giao điểm EF và (I), M là trung điểm BC
Ta có:  (XYFP)=D(XYFP)=I(BCdM)=-1

Vậy tiếp tuyến tại X, Y, và FP cũng đồng quy.
Ta có đpcm

Nhận xét: Thực ra đây là bài toán ngược của bài toán: Cho tam giác ABC có (I) nội tiếp. (I) tiếp xúc với BC, CA, AB tại D, E, F. EF cắt BC tại P. AD cắt (I) tại L. Khi đó PL là tiếp tuyến thứ 2 của (I).

Đường kính Brocard và tam giác đều " thủy túc "

Bài toán 1: Cho tam giác ABC nội tiếp (O), và K là điểm Lemoine  có J, J' là hai điểm đẳng động . Nếu OK cắt (O) tại Q và R thì (QRJJ')=-1

Chứng minh:

Ta đã chứng minh O,K, J, J' thẳng hàng và do J và J' nghịch đảo nhau đối với (O) nên (QRJJ')=-1

QR được gọi là đường kính Brocard của tam giác ABC

Bài toán 2:

Chứng minh rằng có đúng hai điểm đối với một tam giác sao cho chân đường vuông góc hạ

từ chúng đến ba cạnh của tam giác tạo thành một tam giác đều

Chứng minh:

Theo bài toán 1 điểm có hình chiếu lên 3 cạnh tam giác tạo thành 1 tam giác cân nằm

trên một đường tròn apollonius.
Để có tam gíac đều thì điểm đó phải nằm trên 3 đường tròn apollonius của tam giác tức

là hai điểm đẳng động J, J'

của tam giác

Chú ý : Tam giác đều tạo bởi 3 hình chiếu của điểm J lên ba cạnh của tam giác thường

gọi là tam giác đều " thủy túc " của điểm J

Bài toán 3: Trong tất cả các tam giác đều có đỉnh nằm trên ba cạnh của một tam giác thì tam giác đều

thủy túc của điểm đẳng động thứ nhất J của tam giác có diện tích nhỏ nhất.

Chứng minh:

Nhắc lại định lý Miquel :

Cho tam giác ABC và ba điểm L, M, N nằm trên BC, CA, AB. Khi đó ba đường tròn

(AMN),(BLN),(CLM) đồng quy

Gọi các điểm như trong hình vẽ
Ta có:

$\widehat{JLM}=\widehat{JCM}=\widehat{JL'M} \\ \widehat{JLN}=\widehat{JBN}=\widehat{JL'N'} $

Cộng lại ta được:

$\widehat{MLN}=\widehat{M'L'N'}=60^o$

Phép đồng dạng ( vị tự quay) tâm J với tỷ số $r=\frac{JL'}{JL} \le 1, \alpha=\widehat{LJL'}$

biến tam giác

LMN thành tam giác L'M'N'. Theo bài toán 3 suy ra J là điểm đẳng động thứ nhất.

Dùng định lý Pascal suy biến vào bài toán chia đôi

Ta có định lý Pascal đầy đủ cho lục giác, định lý Pascal suy biến là khi một số các đỉnh trùng nhau.

Ta xét bài toán sau:

Cho tam giác ABC, nội tiếp (O), ngoại tiếp (I). BI cắt AC, (O) lần lượt tại $B_0, B_1$. Tương tự $C_0, C_1$ . Gọi S là giao điểm của $C_0B_1 và B_0C_1$. Chứng minh rằng SI chia đôi BC.

Lời giải:

Đặt $ T \equiv B_0C_0 \cap B_1C_1 $ và $ X \equiv AI \cap BC, Y \equiv AT \cap BC $ .

Áp dụng định lý Pascal suy biến cho lục giác $ AABB_1C_1C$ $ \Longrightarrow AT $ là tiếp tuyến của $ \odot (ABC) $ ,
Để ý rằng $ B_1C_1 $ là trung trực $ AI $ nên $ TA=TI $ . ... $ (\star) $

Ta có: $ YA=YX \Longrightarrow $ Kết hợp với $ (\star) $ Ta có $ TI \parallel XY \equiv BC $ ,
Vì thế từ tứ giác $B_0C_1B_1C_1$ toàn phần suy ra $ I(B,C;T,S)=-1 \Longrightarrow IS $ đi qua trung điểm $ BC $ .

Định lý Brocard để chứng minh bài toán liên quan đến trực tâm

Bài toán: Cho tam giác 
$ABC$ nhọn với đường cao $AD,BE,CF$ đồng quy tại $H$. $DE,DF$ lần lượt cắt $AB,AC$ tại $P,Q$. $R$ là trung điểm $PQ$. $N$ là tâm đường tròn ngoại tiếp tam giác $DEF$. Gọi $HN$ cắt $AR$ tại $L$. Chứng minh rằng trực tâm tam giác $ALN$ nằm trên $EF$.

Lời giải:

Gọi $X,Y$ lần lượt là trung điểm của $AC,AB.K$ là giao điểm của $XY$ với $EF$. Ta sẽ chứng minh $K$ là trực tâm của tam giác $ALN$.

Ta có $QF.QD=QA.QC$ nên $Q$ thuộc trục đẳng phương của $(ABC)$ và $(N)$. Tương tự ta suy ra $PQ$ là trục đẳng phương của $(ABC)$ và $(N)$.

Do đó $PQ$ vuông góc với đường thẳng $Euler$ của tam giác $ABC$.




Gọi $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$. Do $KX.KY=KE.KF$ nên $K$ thuộc trục đẳng phương của $(AO)$ và $(AH)$.

Từ đó $AK$ vuông góc với đường thẳng $Euler$ của tam giác $ABC$ hay $AK\parallel PQ$. Mặt khác do $AK\perp OH$ nên $AK\perp NH$

Theo định lí $Brocard$ ta suy ra $EY,FX$ cắt nhau trên $OH$. Lại có $A(QPRK)=-1$ nên $A(QLRK)=-1$ từ đó $L$ là giao điểm của $EY,FX$.

Theo định lí $Brocard$ ta có điều phải chứng minh. $\blacksquare$

4 Cách chứng minh cho bài hình học APMO 2000

Bài toán: Cho  với trung tuyến  và phân giác . Đường thẳng vuông góc với  tại  cắt lần lượt tại . Đường thẳng vuông góc với  tại  cắt tại . Chứng minh: .

Lời giải 1.

---

Một cách tự nhiên ta nghĩ tới việc kéo dài  cắt  tại H.

Ta xét thêm PQ cắt  tại  ()

Ta thấy:  là trung điểm của  mà   (Tính chất hàng điểm điều hòa)

 (Hệ thức Newton)

Mà 

Mà   là trực tâm của 

 (đpcm).

Lời giải 2

Lời giải 3 (Khá giống lời giải 1 nhưng ý tưởng là chứng minh trùng và dùng cực, đối cực)

Giả sử đường thẳng qua O vuông góc BC cắt PR tại Q', Gọi E là giao điểm của đường thẳng qua A song song BC (đặt là l ) và PR.
Xét cực đối cực với (O)
Ta có Q thuộc đường đối cực của A nên A thuộc đường đối cực của Q nên l là đường đối cực của Q. (do l vuông góc OQ).

Từ đó do E là cực của AQ (Do đường đối cực của A là PR, đường đối cực của Q là l)

Gọi M' là giao AQ và BC. thì ta có:

 

Vậy M' là trung điểm BC. Suy ra Q trùng Q'. đpcm

Cách 4: Giả sử đường thẳng qua C và song song với AN cắt tia BA tại C'. 
Từ B kẻ đường vuông góc C'C cắt C'C tại T và tia AN tại U. 
Gọi A' là trung điểm CC'
Qua C kẻ đường thẳng song song với BT, đường này cắt bA ở V
Gọi chân đường thẳng vuông góc kẻ từ V xuống BT là W. Như thế CVWT là hình chữ nhật
AU là phân giác góc CAV và CV vuông góc với AU, nên U là trung điểm WT. 
Suy ra giao điểm N của AU và CW là tâm của hình chữ nhật CVWT, N chính là trung điểm CW. 
Ta đã có M là 
trung điểm BC. Vì M, N lần lượt là trung điểm các cạnh CB và CW của tam giác CBW nên
MN=BW/2
Do CC' song song AN ta có:
$\angle CC'A= \angle BAN= \angle CAN = \angle C'CA$
do đó AC'=AC.  Khi đó AU=C'T-C'A'. Mà N là tâm của hình chữ nhật CTWV nên $NU=\frac{1}{2}CT$ và

$AN=AU-NU=C'T-C'A'-\frac{1}{2}CT=\frac{1}{2}C'T$

Suy ra: $\frac{MN}{AN}=\frac{BW}{C'T}$ Nhưng MN song song với BW và NP nên:

$\frac{QN}{AN}=\frac{MN}{AN}=\frac{BW}{C'T}$

Bây giờ, ta có AN// VW và NP//BW, do đó các tam giác ANP và tam giác VWB đồng dang, và suy ra:

$\frac{AN}{NP}=\frac{VW}{BW}=\frac{CT}{BW}$

Từ đó ta được: $\frac{QN}{NP}=\frac{QN}{AN}.\frac{AN}{NP}=\frac{CT}{C'T}$

PN là đường cao của tam giác vuông ANO, nên hai tam giác ANP và PNO đồng dang. Từ đây ta suy ra:
$\frac{NP}{NO}=\frac{NA}{NP}$

Mặt khác, hai tam giác ANP và C'TB đồng dạng nên ta có:

$\frac{NA}{NP}=\frac{C'T}{BT}$

Do đó $\frac{QN}{NO}=\frac{QN}{NP}.\frac{NP}{NO}=\frac{CT}{C'T}.\frac{C'T}{BT}=\frac{CT}{BT}$

Ta lại có $\angle CTB$ và $\angle QNO$ là hai góc vuông nên hai tam giác $QNO$ và CTB đồng dạng, mà $NO 'perp BT$, do đó $QO \perp BC$