Tổ hợp trong trại hè Hùng Vương

Bài 1: Một hội nghị Toán học quốc tế có 2011 nhà toán học tham dự. Biết rằng một nhà toán học bất kì trong số đó quen biết ít nhất với 1509 nhà toán học khác. Hỏi có thể lập ra một tiểu ban gồm 5 nhà toán học mà người bất kì trong 5 người đó đều quen biết những người con lại của tiểu ban đó hay không ?

Lời giải

Gọi S là tập các nhà Toán học trong hội nghị thì |S|=2011. Giả sử $x,y \in S$, ta quy ước nếu x,y quen biết nhau thì viết (x;y)=1. Xét $a,b \in S$ mà $(a;b)=1$. Đặt:

$A=\left \{ c\in S|c \ne b, (c,a)=1 \right \},B= \left \{c \in S| c \ne a, (c,b)=1 \right \}$

Thì $|A|, |B| \ge 1508, |A \cup B| \le 2009$

Suy ra: $|A \cap B|=|A|+|B|-|A \cup B| \ge 1007$ Do đó tồn tại $c \in A \cap B$, tức là tồn tại 3 nhà toán học a,b,c đôi một quen biết nhau.

Xét:$C=\left \{ d \in S|d \ne a, d\ne b,(d,c)=1 \right \}$ thì $|C| \ge 1507$ và $|(A \cap B) \cup C| \le 2009$ Suy ra:

$|A \cap B \cap C |=|A \cap B|+|C|-|(A \cap B) \cup C| \ge 505$ Do đó tồn tại $d \in A \cap B \cap C$ chứng tỏ có 4 nhà toán học a,b,c,d đôi một quen nhau. Tương tự xét $D$

Ta thu được $|A \cap B \cap C \ cap D| \ge 505+1506-2009=2$

Do đó tồn tại $e \in A \cap B \cap C \cap D$, chứng tỏ có 5 nhà toán học a,b,c,d,e đôi một quen biết nhau. Vậy có thể lập ra một tiểu ban gồm 5 nhà toán học mà bất kì trong 5 người đó đều quen biết những người còn lại của tiểu ban đó.

Bài 2: Trên đường tròn (C) có 2011 điểm. Hỏi có bao nhiêu cách xóa đi 11 điểm sao cho không có hai điểm bị xóa nào cạnh nhau.

Lời giải

Ta gọi một trong số 2011 điểm là A. Có hai trường hợp sau:

Trường hợp 1: Điểm A không bị xóa. Sau khi xóa 11 điểm còn lại 2000 điểm. Xen kẽ giữa 2000 điểm này có 2000 khoảng trông. Mười một điểm bị xóa tương ứng với 11 trong số 2000 khoảng trống nói trên. Do đó số cách thực hiện trong trường hợp này là:

$C^{11}_{2000}$

Trường hợp 2. Điểm A bị xóa. Sau khi xóa tiếp 10 điểm, còn lại 2000 điểm. Xen kẽ những 2000 điểm này có 1999 khoảng trống không kề với vị trí của điểm A. 10 điểm bị xóa (không kể điểm A) tương ứng với 10 trong số 1999 khoảng trống nói trên. Do đó số cách thực hiện trong trường hợp này bằng:

$C^{10}_{1999}$

Theo quy tắc cộng, cách xóa cần tìm thỏa mãn đề bài là:

$C^{11}_{2000}+C^{10}_{1999}$

Hai bài số học của Mỹ và Trung Quốc.

1/ (Mỹ) Chứng minh rằng với mỗi số nguyên $n \ge 2$ đều tồn tại một tập S gồm n số nguyên thoả mãn $(a-b)^2$ là ước của ab với mọi a,b thuộc S phân biệt.
2/ ( Trung Quốc) Tìm số nguyên không âm K nhỏ nhất sao cho với mọi tập con K- phần tử của tập hợp {1,2,..50} tồn tại hai phần tử a,b phân biệt mà a+b là ước của ab

Giải

1/ Ta chứng minh bằng quy nạp rằng với mỗi số nguyên dương n đều tồn tại một tập hợp $S_n$ gồm n phần tử thoả mãn điều kiện đã cho.

Với n=2 chọn $S_2$={0,1}. Giả sử khẳng định đã đúng đến n. Ta chứng minh khẳng định đúng với n+1. Gọi L là BCNN của các số khác 0 có dạng $(a-b)^2$ và ab trong đó $a,b \in S_n$. Đặt:

$S_{n+1}$={$s+L: s \in S_n$} $\cup ${0}

Khi đó, vì $L \ge 0$ nên $S_{n+1}$ chứ n+1 phần tử phân biệt không âm. Ta chứng minh tập $S_{n+1}$ thoả mãn.

Lấy u,v, bất kì. Nếu trong u,v có một số bằng 0 thì hiển nhiên. Nếu u,v đều khác 0 thì tồn tại hai phần tử a,b thuộc S sao cho
$u=L+a, v=L+b.$

Từ các chọn ta có $uv \vdots (u-v)^2$. Vậy ta đã chứng minh với n+1. Theo nguyên lí quy nạp ta có đpcm
2/ Giá trị nhỏ nhất của k=39. Cho a,b thuộc S thoả mãn a+b chia hết ab. Đặt $c=(a,b), a=ca_1, b=cb_1$ thì $(a_1,b_1)=1$ Khi đó $c(a_1+b_1)$ chia hết $c^2a_1b_1$ Suy ra $a_1+b_1$ chia hết $ca_1b_1$. Vì $a_1, b_1$ không có ước chung nên $a_1+b_1$ không chia hết $a_1$ và $b_1$. nên c chia hết cho $a_1+b_1$.(1)

Vì S là tập con {1,..,50}, ta có $a+b \le 99$, vì thế $c(a_1+b_1) \le 99$, từ (1) suy ra $a_1+b_1 \le 9$ mặt khác, $a_1+b_1 \ge 3$ từ đây ta tìm được các cặp (a,b):



(6, 3); (12, 6); (18, 9); (24, 12); (30, 15); (36, 18); (42, 21); (48, 24);

(12, 4); (24, 8); (36, 12); (48, 16)

(20, 5), (40, 10), (15, 10), (30, 20), (45, 30)

(30, 6)

(42, 7), (35, 14), (28, 21)

(40, 24)

(45, 36)


Có 23 cặp, 24 số. Còn lại 26 số. Suy ra K>26. Ta cần tìm giá trị nhỏ nhất của K-26 sao cho ta sẽ chọn được hai số trong 24 số thuộc 1 cặp. Ta tìm được giá trị 13 là nhỏ nhất .Thật vậy, giả sử nhỏ hơn 12 thì ta chọn 26 số đó với các số sau đây 3,4,5,7,8,9,10,14,16,28,30,36.


Vậy K nhỏ nhất là 39.

Dùng phép song ánh để chứng minh bài toán tổ hợp- Phần 2

Hôm nay ta tiếp tục dùng phép song ánh để giải bài toán đếm trong tổ hợp.

Ví dụ 2: Cho tập A={1,2,..,2n}. Một tập con B của A gọi là một tập cân nếu trong tập đó số các số chẵn và các số lẻ bằng nhau. ( Tập rỗng là một tập cân). Tính số tập cân của A.

Giải.
Gọi N là họ các tập con của A có đúng n phần tử, B là một tập cân. $B_1, B_2$ tương ứng các tập số chẵn và lẻ của B thì $B_1=B_2$.

Ta xây dựng một ánh xạ như sau;

$f: B \rightarrow  N$

Trong đó $f(B)=B_1 \cup (Y\setminus B_2)$

$\Rightarrow |f(B)|=|B_1|+|Y|-|B_2|$ vậy muốn cho $f(B)$ thuộc $N$ thì trước hết $Y$ phải có n phần tử và Y không có phần tử chung với $B_1$. Như vậy $Y$ phải tập tất cả số lẻ của tập $A$ ($|Y|=n)$

Nên f đơn ánh

Nếu có tập $M$ thuộc $N$. Kí hiệu $M_1$, $M_2$ là tập số chẵn số lẻ của M thì $|M_1|+|M_2|=n$. Ta phải tìm xây dựng $B_1,B_2$ theo $M_1, M_2$ sao cho $|B_1|=|B_2|$ thì $B_2=Y \setminus M_2$ và $B_1=M_1$. $\Rightarrow f(B)=M$.

Như vậy ta xây dựng song ánh giữa B và N.

Vậy A có tấp cả $C^n_{2n}$

Nhận xét: Tại sao lại xây dựng f đi từ B đến N ? Thực ra qua một vài phép liệt kê ta sẽ thấy !
Một số bài tập cho bạn đọc:

1/(Bài toán chia kẹo của Euler) Có m chiếc kẹo giống nhau chia cho n em bé. Hỏi có bao nhiêu cách chia?

Đây cũng chính là bài toán: “Tìm số nghiệm không âm của phương trình : 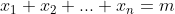 ($n, m \in N^*$). 

Các bạn có thể nghiên cứu chuyên đề tại đây.

2( Lấy trong TLCT)/ Cho trước số nguyên dương n và số nguyên dương r thoả $r<n-r+1$. Giả sử X={1,2..n}. Hoi r có bao nhiêu tập con A của X đồng thời có tính chất:

+ Chứa r phần tử

+ Không chứa hai số nguyên liên tiếp.

(Gợi ý: Các bạn thử liệt kê như Vd 2 các bạn sẽ có hướng làm).