Cực và đối cực trong bài toán.

Đề: Cho tam giác ABC có I là tâm nội tiếp, Q là tiếp điểm trên AC, E là trung điểm AC. K là trực tâm của tam giác BIC. CM: KQ vuông IE.

Lời giải:

Cách 1: Gọi $F$ là trung điểm $AB$ Gọi $(I)$ tiếp xúc $BC$ tại $P.$ Nếu $BI$ cắt $EF$ tại $L,$ Ta có $\widehat{FLB}=\widehat{LBC}=\widehat{FBL}$ $\Longrightarrow$ $\triangle FBL$ cân tại F $\Longrightarrow$ $FA=FB=FL$ $\Longrightarrow$ $\widehat{ALB}=90^{\circ}$ $\Longrightarrow$ $AQLI$ is cyclic $\Longrightarrow$ $\widehat{CQL}=\widehat{AIL}=90^{\circ}-\tfrac{1}{2}\widehat{ACB}=\widehat{CQP}$ $\Longrightarrow$ $L \in PQ,$ i.e. $L$ nằm trên đường đối cực của $C$ đối với $(I)$, nên C thuộc đường đối cực của L mà $CK \perp IL$ nên CK là đường đối cực của $L$ đối với $(I)$, suy ra đường đối cực của K sẽ là đường thẳng qua L $\Longrightarrow$ $ELF \perp IK$ là đường đối cực của $K$ đối với $(I)$ , ta có Q là đường đối cực của E đối với (I) $\Longrightarrow$  $KQ$ đường đối cực của $E$ đối với $(I)$ $\Longrightarrow$ $KQ \perp IE,$ dpcm.

Cách 2:Gọi$P$ là tiếp điểm của đường tròn bàng tiếp góc B với $AC$. Khi đó $ \angle KIQ=\angle C=\angle BCP$ và \[ \frac{BC}{CP}=\frac{KI}{IQ}. \]
Vì thế $ \triangle CBP \sim \triangle QKI $ và $ \angle IKQ=\angle CBP$ $ \Rightarrow $ $ KQ\perp BP $.

mà $BP\parallel IE$, nên $KQ\perp IE$.

Phép nghịch đảo để chứng minh thẳng hàng

Bài toán: Gọi $ H,O$ là trực tâm và tâm ngoại tiếp $ \Delta ABC$. Đường tròn ngoại tiếp và đường tròn Euler của $ \Delta HBC$ cắt nhau tại $ \{M,N \}$. Gọi $ O^*$ là tâm đường tròn ngoại tiếp $ \Delta AMN$ và $ L$ là trung điểm của $ OA$. Chứng minh rằng $ H,O^*,L$ thẳng hàng            

Lời giải:

Gọi    $ A’,B’,C’$ là chân đường cao đến các cạnh $ BC,CA,AB.$ $ F$ là trung điểm $ BC$  Gọi $ B’C’$ cắt $ BC$ tại $ P$ và cắt $ (O)$ tại $ B’',C’'.$ Vì $ (B,C,A’,P) =- 1,$ nên  $ PB \cdot PC = PA’ \cdot PF$ $ \Longrightarrow$ $ PB’' \cdot PC’' = PA’ \cdot PF$ $ \Longrightarrow$ $ F \in \odot(A’B’'C’').$ Vì thế tâm của $ \odot(A’B’'C’')$ là đường thẳng qua vuông góc từ $ A$ đến $ B’C’$ giao với trung trực $ A’F,$ chính là trung điểm $ L$ của $ AO.$ Phép nghịch đảo $ \mathcal{I}$ tâm $ H,$ biến $ (O)$ thành đường tròn chín điểm $ \mathcal{N},$ và biến $ B’C’$ thành đường tròn ngoại tiếp $ \triangle HBC$ và $ \odot(A’B’'C’')$ thành đường tròn đi qua $ A$ và Giao điểm $M,N$ của $ \mathcal{N}$ và $ \odot(HBC),$ Là ảnh của $ A’,C’',B’'$ $ \Longrightarrow$ phép nghịch đảo tâm $ H,$ biến tâm ngoại tiếp $ L$ của $\odot (A’B’'C’')$ và tâm $ O^*$ của tam giác $ \odot(AMN)$ thẳng hàng.

Ứng dụng bổ đề ERIQ

Bài toán 1: Tam giác ABC không cân $\Delta ABC$. $E,F$ là các chân đường cao từ $B,C$ trên $AC,AB$, H là trực tâm
$E,Q$ trên $[FB);[EC)$ sao cho: $FP=FC; EQ=EB$
$BQ$ cắt $CP$ tại $K$.
$I,J$ là trung điểm của $BQ,CP$.
$IJ$ cắt $BC,PQ$ tại $M,N$
1/ Chứng minh: $HK\bot IJ$
2/ $\widehat{PAM}=\widehat{QAN}$

Lời giải:

Ta có $\overline{HF}.\overline{HC}=\overline{HE}.\overline{HE}$
Nên $H$ thuộc trục đẳng phương của $[CP]$ và $[BQ]$
$BCQP$ là tứ giác nội tiếp nên $\overline{KC}.\overline{KP}=\overline{KB}.\overline{KQ}$
Vì thế $K$ thuộc trục đẳng phương $[CP]$ và $[BQ]$
Vậy $HK\perp IJ$
(b)
Ta có $\dfrac{\overline{IQ}}{\overline{IB}}=\frac{\overline{JP}}{\overline{JC}}$
Áp dụng bổ đề ERIQ được: $\dfrac{\overline{BM}}{\overline{MC}}=\dfrac{\overline{QN}}{\overline{NP}}\Rightarrow đpcm$



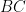Bài toán 2 (Juliel blog) : Cho tứ giác nội tiếp được đường tròn. Gọi lần lượt là các giao điểm của và , và 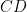. Gọi là giao điểm của phân giác hai góc 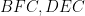. lần lượt là trung điểm của . Chứng minh rằng thẳng hàng.

Lời giải :



Gọi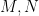 lần lượt là giao điểm của với .

Ta sẽ chứng minh .

Thật vậy, ta có



Mà trong tam giác thì cũng là phân giác, do đó nó cũng là trung tuyến, hay .

Theo tính chất phân giác :



Mà theo hệ thức lượng trong đường tròn thì

Suy ra

Xét hai bộ ba điểm thẳng hàng các điểm 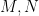lần lượt thuộc và thỏa mãn (chứng minh trên)

Các điểm lần lượt thuộc và thỏa

Như vậy theo bổ đề ta có thẳng hàng. Đây là điều phải chứng minh.