Bất đẳng thức 3 biến đối xứng có hình thức đẹp và nhiều ý tưởng giải hay. Có lẽ vì thế mà chúng xuất hiện nhiều trong các kỳ thi trong và ngoài nước. Đã có khá nhiều phương pháp mạnh giải quyết loại bài toán này như: SCHUR, SOS, SS, MV, EV , GLA,PHƯƠNG PHÁP DỒN BIẾN…..Trong bài viết này tôi sẽ trình bày một phương pháp mới gần gũi hơn với học sinh THPT “PHƯƠNG PHÁP SỬ DỤNG HÀM SỐ BẬC 1, BẬC 2”.
1. Bất đẳng thức đối xứng 3 biến trên 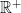
1.1. Cơ sở lý thuyết
Chúng ta đã biết hàm số bậc nhất đạt giá trị lớn nhất hay nhỏ nhất tại biên. Hàm số bậc 2 hệ số a dương đạt giá trị lớn nhất tại biên và hệ số a âm thì đạt giá trị nhỏ nhất tạ biên. Dựa vào đặc điểm này ta sẽ quan tâm việc đi tìm đặc điểm biên của biến trong bài toán nhiều biến số . Cụ thể là hàm số 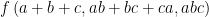 đạt giá trị lớn nhất, nhỏ nhất khi và chỉ khi có 1 biến bằng 0 hoặc 2 biến bàng nhau.
đạt giá trị lớn nhất, nhỏ nhất khi và chỉ khi có 1 biến bằng 0 hoặc 2 biến bàng nhau.
Trước hết ta xét 2 bài toán cơ bản sau
Bài toán 1. Cho các số thực không âm 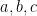 thõa mãn
thõa mãn
Tìm giá trị lớn nhất , giá trị nhỏ nhất của biểu thức 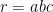
Lời giải. Xét phương trình
Ta cần tìm r để phương trình (1) có 3 nghiệm không âm. Đặt
Vì 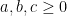 khi và chỉ khi
khi và chỉ khi 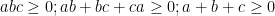 . Nên phương trình (1) có 3 nghiệm không âm
. Nên phương trình (1) có 3 nghiệm không âm
Hay
Từ đó ta có giá trị lớn nhất của  là
là 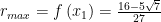 . Dấu đẳng thức xảy ra khi và chỉ khi
. Dấu đẳng thức xảy ra khi và chỉ khi
và các hoán vị
và 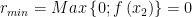 . Dấu đẳng thức xảy ra khi và chỉ khi:
. Dấu đẳng thức xảy ra khi và chỉ khi:
và các hoán vị
Nhận xét. Lời giải bài toán 1 không có gì mới lạ nếu như ta nhìn xoáng qua. Xong nếu để ý dấu đẳng thức xảy ra và khai thác ta sẽ có cách nhìn tổng quát về cả một dạng toán như tiêu đề bài viết.
Bài toán 2.(tổng quát của bài toán 1) Cho các số thực không âm 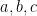 thõa mãn
thõa mãn
Tìm giá trị lớn nhất , giá trị nhỏ nhất của biểu thức 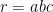 theo
theo 
Gợi ý: Tương tự lời giải bài toán 1 ta có kết quả
Bây giờ ta đi vào trọng tâm của bài viết. Tìm đặc điểm, mối quan hệ của các biến khi hàm số đạt giá trị lớn nhất , nhỏ nhất
Định lý . Mỗi bộ số thực không âm 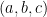 luôn tồn tại 1 trong 2 bộ
luôn tồn tại 1 trong 2 bộ  và
và  thỏa mãn đông thời 3 điều kiện
thỏa mãn đông thời 3 điều kiện
i) 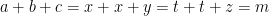
ii) 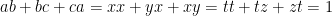
iii) 
Chứng minh. Ta chứng minh trong trường hợp tồn tại giá trị lớn nhất 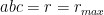 . (trường hợp còn lại chứng minh tương tự)
. (trường hợp còn lại chứng minh tương tự)
Xét phương trình
Đặt
Để ý:
Nên  có 2 nghiệm kép
có 2 nghiệm kép 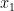 . Từ đó ta chọn bộ
. Từ đó ta chọn bộ  là
là 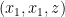
(Sự tồn tại một trong 2 bộ là sự tồn tại 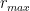 ,
, và các biến phải thuộc
và các biến phải thuộc 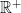 bạn đọc tự chứng minh, điều đó cũng được thể hiện rõ trong yêu cầu bài toán chứng minh bất đẳng thức hay tìm giá trị lớn nhất , nhỏ nhất)
bạn đọc tự chứng minh, điều đó cũng được thể hiện rõ trong yêu cầu bài toán chứng minh bất đẳng thức hay tìm giá trị lớn nhất , nhỏ nhất)
Nhận xét : Định lý vẫn đúng trong trường hợp
Hệ quả . Đa thức đối xứng 3 biến 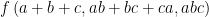 là hàm bậc 1 hoặc bậc 2 theo
là hàm bậc 1 hoặc bậc 2 theo  thì đạt giá trị nhỏ nhất (hệ số a âm)hoặc lớn nhất (hệ số a dương )khi và chỉ khi 1 trong 3 biến bằng 0 hoặc 2 biến bằng nhau
thì đạt giá trị nhỏ nhất (hệ số a âm)hoặc lớn nhất (hệ số a dương )khi và chỉ khi 1 trong 3 biến bằng 0 hoặc 2 biến bằng nhau
Chú : trong trường hợp bậc lớn hơn 2 thì ta thay bởi điều kiện 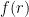 là hàm lồi hay lõm điều này được sử dụng trong thi HSG QG
là hàm lồi hay lõm điều này được sử dụng trong thi HSG QG
Chứng minh: Hàm bậc 1 thì giá trị lớn nhất hay nhỏ nhất đạt được tại biên. Hàm bậc hệ số a dương đạt giá trị lớn nhất tại biên, hệ số a âm đạt giá trị nhỏ nhất tại biên. Từ định lý ta suy ra khi  tại biên khi và chỉ khi 2 biến bằng nhau hoặc một biến bằng 0 (Trong trường hợp a,b,c là ác số thực thì chỉ xảy ra khi 2 biến bằng nhau)
tại biên khi và chỉ khi 2 biến bằng nhau hoặc một biến bằng 0 (Trong trường hợp a,b,c là ác số thực thì chỉ xảy ra khi 2 biến bằng nhau)
1.2. Một số đẳng thức thường sử dụng
Với 3 biến  . Đặt
. Đặt  ,
,  ,
,  . Ta có các đẳng thức sau
. Ta có các đẳng thức sau
1.3. Bài tập vận dụng
Bài 1. Cho các số thực dương 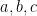 . Chứng minh rằng
. Chứng minh rằng
Lời giải.
Chuẩn hóa 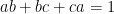 . Đặt
. Đặt 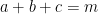 ,
, 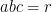 . Ta có
. Ta có
Bất đẳng thức cần chứng minh trở thành
Với 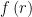 là hàm số bậc nhất có hệ số a dương nên đạt giá trị lớn nhất khi
là hàm số bậc nhất có hệ số a dương nên đạt giá trị lớn nhất khi 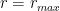 . Áp dụng bổ đề 1ta có
. Áp dụng bổ đề 1ta có 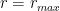 khi và chỉ khi có 2 trong 3 số
khi và chỉ khi có 2 trong 3 số 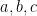 bằng nhau. Giả sử
bằng nhau. Giả sử 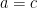 . Bất đẳng thức ban đầu cần chứng minh trở thành
. Bất đẳng thức ban đầu cần chứng minh trở thành
Việc biến đổi sau khi xét 2 biến bằng nhau một cách khéo léo ta cần để ý đến nhân tử  khi đẳng thức xảy ra tại 3 biến bằng nhau
khi đẳng thức xảy ra tại 3 biến bằng nhau
Bài 2. Cho các số thực dương 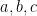 . Chứng minh rằng
. Chứng minh rằng
Lời giải:
Chuẩn hóa 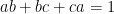 . Đặt
. Đặt 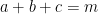 ,
, 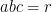 . Ta có
. Ta có
Biểu diễn bất đẳng thức đã theo các biến mới 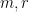 ta được
ta được
Với 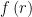 là hàm số bậc nhất có hệ số a dương nên đạt giá trị lớn nhất khi
là hàm số bậc nhất có hệ số a dương nên đạt giá trị lớn nhất khi 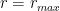 . Áp dụng hệ quả ta có
. Áp dụng hệ quả ta có 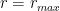 khi và chỉ khi có 2 trong 3 số
khi và chỉ khi có 2 trong 3 số 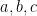 bằng nhau. Giả sử
bằng nhau. Giả sử 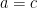 . Bất đẳng thức ban đầu cần chứng minh trở thành
. Bất đẳng thức ban đầu cần chứng minh trở thành
Bài 3.[ Rusia MO-2005] Cho các số thực không âm 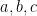 thõa mãn
thõa mãn
Chứng minh rằng
Nhận xét.
i) Đây là bất đẳng thức 3 biến đối xứng. Nếu ta qui đồng mãu thì sẽ đưa về đa thức đối xứng bậc 9 đối với 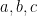 và bậc 3 đối với
và bậc 3 đối với 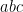
ii) Điều kiện bài toán không cho ta 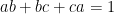
Tuy nhiên ta có thể xử lý bài toán bằng cách đổi biến để được như ý muốn dùng hệ quả như sau :
Đặt  . Bài toán đã cho trở thành .Cho
. Bài toán đã cho trở thành .Cho 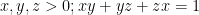 . Chứng minh rằng
. Chứng minh rằng  . Đến đây ta đã được đủ điều kiện sử dụng bổ đề 2 và chỉ cần xét 2 trường hợp khi có 2 biến bằng nhau hoặc 1 biến bằng 0. Cụ thể là việc làm quá đơn giản.
. Đến đây ta đã được đủ điều kiện sử dụng bổ đề 2 và chỉ cần xét 2 trường hợp khi có 2 biến bằng nhau hoặc 1 biến bằng 0. Cụ thể là việc làm quá đơn giản.
Bài 4. [Iran 96] Cho các số thực dương 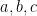 . Chứng minh rằng
. Chứng minh rằng
Hướng dẫn: Sử dụng các đẳng thức ở trên ta được  bậc 2 có hệ số a âm. Nên áp dụng được hệ quả
bậc 2 có hệ số a âm. Nên áp dụng được hệ quả
Bài 5. Cho 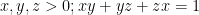 . Chứng minh rằng
. Chứng minh rằng
Bài 6. Cho các số thực dương  Chứng minh rằng
Chứng minh rằng
Bài 7. [Vietnam TST]. Cho các số thực 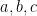 . Chứng minh rằng
. Chứng minh rằng
Bài 8. Cho các số thực không âm 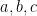 thõa mãn
thõa mãn
Chứng minh rằng
Câu hỏi mở thú vị.
Nếu như các biến a,b,c bị ràng buộc bởi các điều kiện khác nhau: Chẳng hạn abc=1, ab+bc+ca+abc=4,….thì bạn sẽ xử lý thế nào?
Tôi sẽ trình bày trong thời gian tới . Thân ái !
Không có nhận xét nào:
Đăng nhận xét